Curve of constant precession

CURVE OF CONSTANT PRECESSION

Curve studied by Paul D. Scofield in 1995.

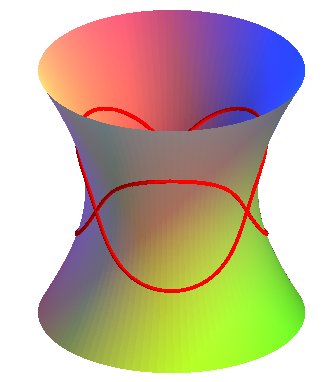
Cartesian parametrization:

where

Curve traced on the hyperboloid: .
Curvilinear abscissa: .
Radius of curvature: , radius of torsion: .
Intrinsic equation: .
Instant rotation vector: .

The curves of constant precession are the curves such that the instant rotation vector of the Frenet frame has a motion of uniform rotation around a fixed axis when this frame travels along the curve at constant speed. Therefore, this vector has a motion similar to that of the axis of a spinning top, hence the expression "constant precession".

Remember that if the Frenet frame is written , then the instant rotation vector is defined by the relations: and given by the formula: .

The projection on the plane xOy of the curve given above is an epitrochoid with parameter .
Opposite, the case k =3/5 which gives q = 3.

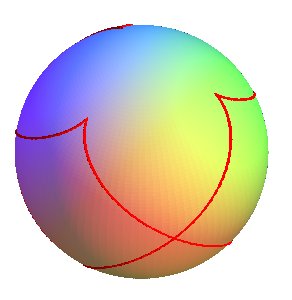
The end of the tangent vector describes the spherical indicatrix of curvature of the curve; the formulas
show that this indicatrix is a spherical helix.
Opposite, the indicatrix of curvature of the curve above.

Compare to the Capareda curves.

next curve previous curve 2D curves 3D curves surfaces fractals polyhedra

The projection on the plane xOy of the curve given above is an epitrochoid with parameter . Opposite, the case k =3/5 which gives q = 3.
The end of the tangent vector describes the spherical indicatrix of curvature of the curve; the formulas show that this indicatrix is a spherical helix. Opposite, the indicatrix of curvature of the curve above.