La courbe  du plan xOy se relève sur la surface  en la courbe . La courbe  se relève sur la surface de révolution  en la courbe .

Le relèvement d'une courbe plane sur une surface est l'intersection du cylindre construit sur la courbe orthogonalement à son plan, avec la surface. C'est donc la courbe maximale tracée sur la surface qui se projette orthogonalement sur la courbe.

Exemples :
    - les relèvements de droites sur une surface sont les courbes planes tracées sur la surface.
    - les relèvements de cercle sont les courbes cylindriques.
    - les clélies sont des relèvements de rosaces sur une sphère, alors que les vasques en sont des relèvements sur un paraboloïde hyperbolique, et les rosaces coniques, des relèvements sur un cône de révolution.
    - l'ellipse sphérique est un relèvement d'ellipse sur une sphère.
    - l'hélice conique est un relèvement de spirale logarithmique, tandis que la spirale conique de Pappus est un relèvement de spirale d'Archimède.
    - les hélices sphériques sont des relèvements d'épicycloïdes.
    - les hélices du paraboloïde hyperbolique (placé verticalement) sont des relèvements de développantes de cercle.
    - les géodésiques du cône de révolution sont des relèvements d'épis, et les cercles géodésiques des relèvement de rosaces.
    - les géodésiques de paraboloïde de révolution sont des relèvements d'hypercycloïdes.
 

Relèvements coniques de spirales d'Archimède à gauche, logarithmiques à droite.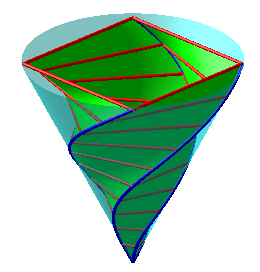
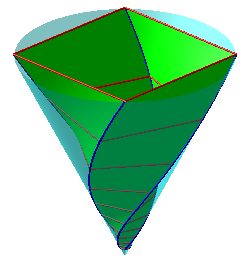Relèvements sur paraboloïde hyperbolique de spirales d'Archimède à gauche, logarithmiques à droite.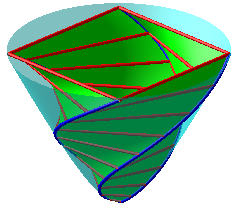

 
 

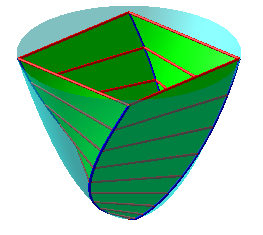courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL  2017