CLÉLIE
Clelia
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
CLÉLIE
Clelia
| Courbe étudiée par Pappus dans un cas particulier,
et par Guido Grandi en 1728 ; ce dernier lui a donné le nom de clélie
en hommage à la comtesse Clelia
Borromeo, et non à l'héroïne légendaire de
Rome, ni à celle d'un roman de Mme de Scudéry !
Autre nom : spirale (d'Archimède) sphérique. |
Équation sphérique : 
( = latitude, 
= longitude).
Paramétrisation cartésienne :  .
Équation cylindrique :  .
Courbe sphérique, algébrique ssi n est rationnel (degré = 2  (numérateur
+ dénominateur de n)).
Abscisse curviligne :  .
Longueur du motif de base : 
(intégrale elliptique). |
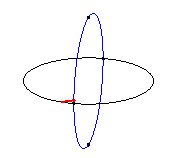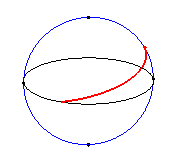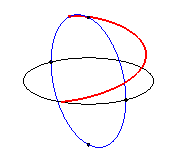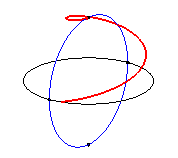
| Les clélies sont les lieux d’un point M
d’un méridien d’une sphère
tournant à vitesse constante
w
autour
de l’axe polaire, le point M se déplaçant à
la vitesse constante nw sur ce méridien.
On obtient donc physiquement une clélie lorsque l'on pèle une orange où lorsqu'on rembobine régulièrement une pelote de ficelle sphérique. Inversement, un vent dirigé vers un pole aura sur la terre une trajectoire de clélie. |
 |
Les clélies sont aussi obtenues par l'intersection
d'un conoïde de Plücker
généralisé :
avec la sphère de centre O et de rayon R.
Ci-contre, le cas n = 3 : l'intersection est formée de 2 clélies symétriques. |
 |
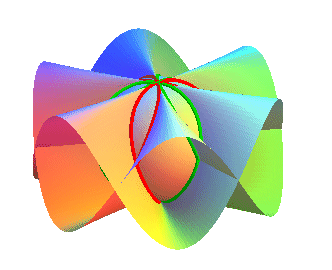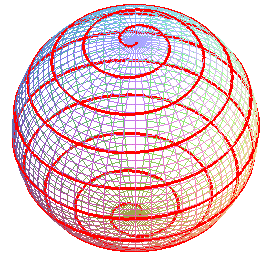
La courbe est formée d'un motif de base (représenté
ci-contre), symétrique par rapport à Ox, obtenu pour  ,
partant du pôle sud pour arriver au pôle nord après
1/(2n) tours ; on obtient la courbe entière en effectuant
toutes les rotations autour de Oz d'angles 
pour k entier suivies chacune de la symétrie par rapport
à xOy.
Lorsque n est rationnel de numérateur p, la courbe est formée de 2p motifs issus du motif de base par les antirotations précédentes pour  .
La courbe est symétrique par rapport à xOy si et seulement numérateur et dénominateur de n sont impairs, sinon elle est symétrique par rapport à O. |
 |
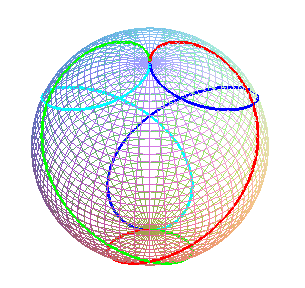
Les 4 motifs rouge, puis bleu, puis cyan, puis vert pour n = 2/3. |
Exemples :
n = 1 : courbe de Viviani. |
n = 2 |
n = 3 |
n = 4 |
n = 5 |
n = 1/2 |
n = 3/2 |
n = 5/2 |
n = 7/2 |
n = 9/2 |
n = 1/3 |
n = 2/3 |
n = 4/3 |
n = 5/3 |
n = 7/3 |
n = 1/4 |
n = 3/4 |
n = 5/4 |
n = 7/4 |
n = 9/4 |
n = 1/5 |
n = 2/5 |
n = 3/5 |
n = 4/5 |
n = 6/5 |
Si vous avez le logiciel Maple et souhaitez manipuler ces figures à la souris, téléchargez ce fichier.
La projection (orthogonale) sur xOy est la rosace
: 
.
La projection conique de centre O sur le plan
z
= R est le noeud : 
.
La projection stéréographique de pôle
sud est le noeud : 
.
La clélie est
la projection cylindrique d'axe Oz sur la sphère de centre
O
et de rayon R de la couronne
sinusoïdale : 
tracée sur le cylindre d'axe Oz et de rayon R. |
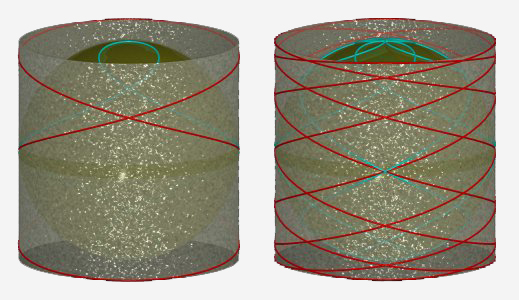
Figure réalisée par Alain Esculier |
Elle est aussi la projection centrale de centre O
de la couronne
tangentoïdale : 
tracée sur le même cylindre. |
 |
Les clélies sont des cas limites des solénoïdes toriques.
Ne pas confondre les clélies avec les hélices
sphériques, ni avec les loxodromies.
| La clélie pour n = 2 est un cas limite de courbe de la balle de tennis ; c'est aussi comme vu ci-dessus, l'intersection du conoïde de Plücker avec une sphère. |
 |
 |
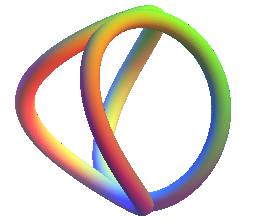La paramétrisation de la sphère : 
a pour lignes de coordonnées les clélies  de
paramètre  . |
 |
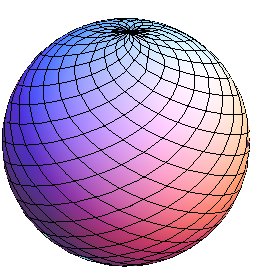| Les mailles de ce filet, formant des carrés lorsqu'il
est applati, forment des courbes ressemblant fort à des clélies
lorsqu'il enserre une boule sphérique.
Cependant, si l'on considère que le filet est formé de mailles inextensibles, et que seuls les angles peuvent varier, la solution mathématique du problème n'est pas un réseau de clélies ; voir ici un tel habillage de la sphère. |
 |
Comparer avec les rosaces
coniques, et les vasques 3D,
qui se projettent également en des rosaces planes.
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2022