next curve previous curve 2D curves 3D curves surfaces fractals polyhedra

CLELIA


Curve studied by Pappus in a special case, and by Guido Grandi in 1728; he is the one who named it clelia as a tribute to the countess Clelia Borromeo, and not to the legendary Roman heroine, or the main character of a novel by Mme de Scudery! 
Other name: spherical (Archimedean) spiral.

 
Spherical equation:  ( = latitude,  = longitude).
 Cartesian parametrization: . 
 Cylindrical equation: . 
 Spherical curve, algebraic iff n is rational (degree = 2(numerator + denominator of n)).
 Curvilinear abscissa: . 
 Length of the base pattern:  (elliptic integral).

 
The clelias are the loci of a point M on a meridian of a sphere rotating at constant speed w around the polar axis, the point M also moving at constant speed nw along this meridian.
Therefore, physically, we obtain a clelia when peeling an orange or when rewinding regularly a spherical wool ball.
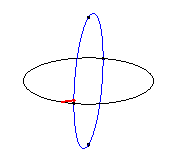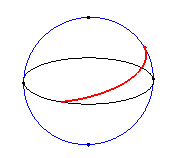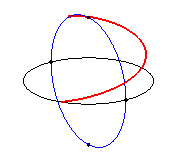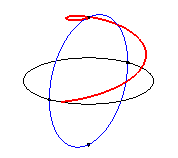The clelias are also obtained as the intersection between a generalized Plücker conoid :  and the sphere with center O and radius R. 
Opposite, the case n = 3: the intersection is composed of 2 symmetrical clelias.

 
 
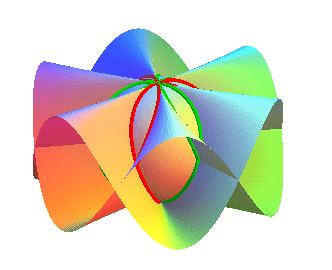The curve is built from a base pattern (represented opposite), symmetrical with respect to Ox, obtained for , that goes from the South to the North pole after 1/(2n) rotations; we get the whole curve by applying all the rotations around Oz of angle , each followed by the symmetry with respect to xOy, for integral values of k ;  is enough if n is rational with numerator p.
The curve is symmetric with respect to xOy iff p and denominator q are odd, otherwise it is symmetric with respect to O. 

When n is rational with numerator p and denominator q,

In this case, the curve is composed of 2p patterns, obtained from the base pattern by rotations of axis Oz and angles  and  + p.

When p and q are odd, the curve is composed of p patterns, obtained from the base pattern by rotations of axis Oz and angles .

Examples:

n = 1: Viviani curve.

n = 2

n = 3 

n = 4

n = 5

n = 1/2 

 n = 3/2

n = 5/2

n = 7/2

n = 9/2

n  = 1/3 

n = 2/3

n = 4/3

n = 5/3

n = 7/3

n = 1/4

n = 3/4

n = 5/4

n = 7/4

n = 9/4

n = 1/5

n = 2/5

n = 3/5

n = 4/5

n = 6/5

If you have the software Maple and wish to manipulate these figures, download this file.

The (orthogonal) projection on xOy is the rose.
The conical projection with center O on the plane z = R is the knot: .
The stereographic projection from the South pole is the knot: .
 
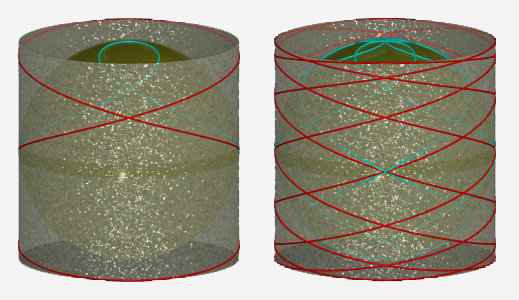
The clelia  is the cylindrical projection with axis Oz on the sphere with center O and radius R of the cylindrical sine wave traced on the cylinder with axis Oz and radius R.
Figure made by Alain Esculier
It is also the central projection with center O of the cylindrical tangent wave traced on the same cylinder.

The clelias are limit cases of torus solenoids.

Do not mistake the clelias for spherical helices, or rhumb lines.
 
 
The clelia for n = 2 is a limit case of the seam line of a tennis ball; it is also, as we've seen above, the intersection between the Plücker conoid and a sphere.

 
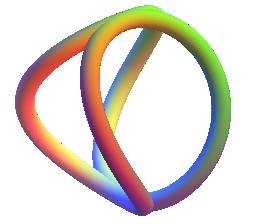The coordinate lines of this parametrization of the sphere:  are the clelias  with parameter .

 
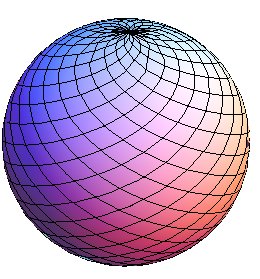The mesh of this net, that creates squares when it is flattened, forms curves that look like clelias when the net encircles a spherical ball. 
Nonetheless, if we consider that the net is made of an inelastic mesh, and that only the angles can vary, then the mathematical solution to this problem is not a lattice of clelias; see here such a dressing of the sphere.

Compare to the conical roses, and the 3D basins, that can also be projected onto planar roses.
 
next curve previous curve 2D curves 3D curves surfaces fractals polyhedra

© Robert FERRÉOL 2018