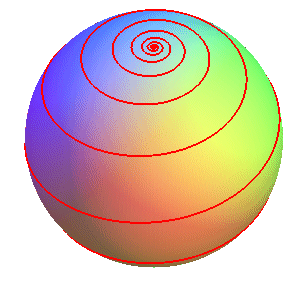
RHUMB LINE OF THE SPHERE
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
RHUMB LINE OF THE SPHERE
| Curve studied by Pedro
Nunes in 1537, Simon
Stevin in 1608, Maupertuis
in 1744; name given by Snellius
in 1624.
Other names: loxodrome, wind line. |
Writing 
= longitude, 
= latitude, 
where 
is the constant angle between the curve and the parallels:
Spherical differential equation:  .
Except the case of the parallels:
= constant obtained for
= 0:
Spherical equation:  .
where gd-1 is the inverse of the Gudermann function, defined for 
by:
gd-1 (x) = ln (tan(x/2 +  /4))
= arsinh(tan x) = artanh(sin x) = sign(x).arcosh(sec(x)),
(the plot of which is the pseudo-elliptic radioid). Cylindrical equation for  : 
(hence the parametrization:  )
Radius of curvature:  .
Radius of torsion:  . |
The rhumb lines of the
sphere,
associated to a given axis, are the curves that form a constant angle with
the parallel (or the meridians).
Do not mistake the rhumb lines for the spherical
helices, that form a constant angle with the equatorial plane, nor
for the clelias.
The rhumb lines correspond to the straight lines in Mercator
coordinates 
;
in other words, on the maps of the Earth that use the Mercator projection,
the rhumb lines are represented by straight lines. The angle a
that the images of the rhumb lines form on the map with respect to the
horizontal is the same as the angle they form on the sphere with respect
to the parallels.
If we know the geographic coordinates 
and 
of
two points, the angle a associated to the shortest
rhumb line joining these two points is obtained by the formula: 
and the length is given by: 
.
The notion of rhumb line is opposed to that of geodesic,
shortest path joining two points on the sphere, which is an arc of a great
circle ; by comparison, the length of the geodesic
joining the two points above is given by the formula 
.
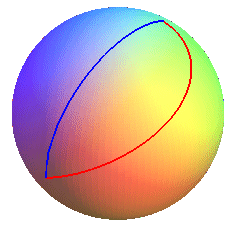 The rhumb line (in red) and the geodesic (in blue) joining the point
with longitude 15° west and latitude 15° south to the point with
longitude 150° west and latitude 60° north.
|
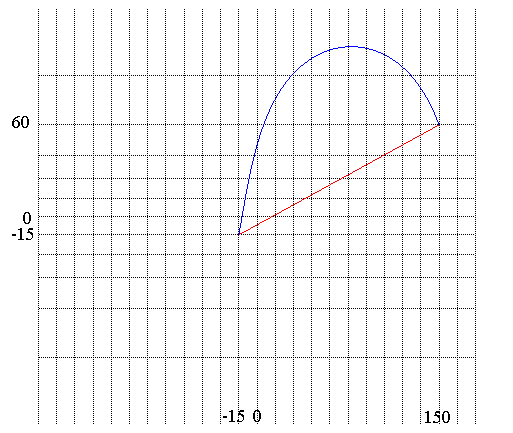
The same on a map in Mercator projection!!! |
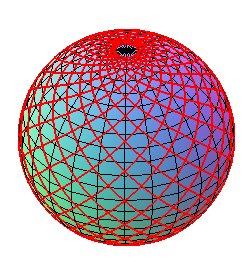
| The double lattice of rhumb lines forming an angle of
±45° with the meridians creates an elegant lattice of orthogonal
curves on the sphere.
Compare to the lattice of Viviani curves. |
 |
 |
 |
| Hemispherical dome photographed from the tower of Pisa.
The center K of a tile on the row n+1 is at a right angle from the junction of the two tiles with centers I and J on the row n, thus IK and JK form 45° angles with the parallel passing by I and J; the consecutive centers of the tiles follow rhumb lines at 45°. Picture: Alain Juhel. |
 |
The orthogonal projection of the rhumb line on the equatorial
plane is, as the above cylindrical equation shows, the unbounded
Poinsot spiral: 
.
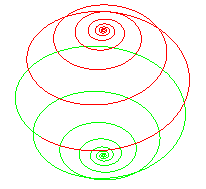
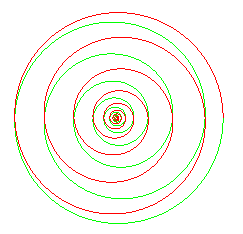
The stereographic projection from the North pole on the
equatorial plane is the logarithmic
spiral: 
,
which forms the same angle 
with the radius vector as the rhumb line forms with the meridians (since
the stereographic projection is a conformal map).
 |
 |
Rhumb lines as seen by Escher
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL, Jacques MANDONNET 2018