Cartesian equation: . Spherical equation: r = R. Cartesian parametrizations:
1)  with , longitude,  latitude.
2) Mercator coordinates, change sin v into th v in 1): ; the curves v = k u are the rhumb lines of the sphere.
3) Stereographic coordinates from the South pole: . The coordinate lines are the sections of the sphere by the planes passing by the lines x = 0, z = -R and y= 0, z = -R. The interest of this parametrization is that it is conformal (preserves the angles).
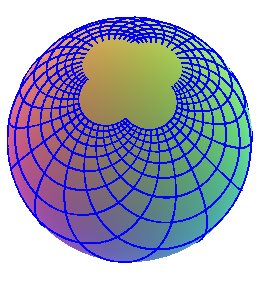4)  the coordinate lines are the clelias: , with parameter .
5) the coordinate lines are the Viviani curves (sections by the cylinders with generatrix Oz and radius R/2); case p = q = 1 of 4).
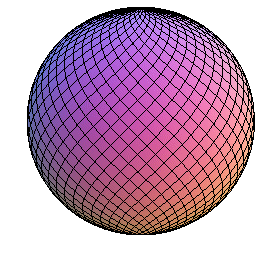5)  has the characteristic of being a "dressing" (E = G = 1) of the northern hemisphere minus the equator and the pole; however, an "isometry" is impossible (E = G = 1 and F = 0). The coordinate lines are studied here.
The spherical parametrization:  where  is a constant and am the Jacobi amplitude function (JacobiAM in Maple), also provides a dressing, this time of the whole sphere minus the poles. The piece of fabric that dresses this sphere is, before deformation, a square with area , minimal for .
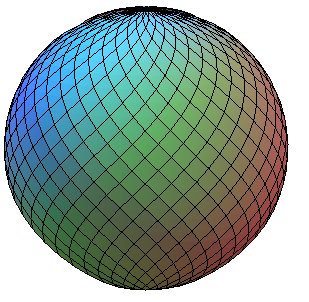First fundamental quadratic form:  Surface element: . Second fundamental quadratic form:  Principal radii of curvature: R and R. Area: ; volume: .

The sphere with center O and radius R is the locus of the points of space located at distance R from O.
It is therefore the surface generated by the revolution of a circle around its diameter, which is a limit case of torus.
NSC: surface all the points of which are umbilics.

The sphere is a surface homeomorphic to the Alexandroff compactification of the plane , written . In other words, the sphere minus one point is topologically equivalent to the plane.

See here the problem of the 13th sphere.

See also the ellipsoid, image of the sphere by an affine transformation.
 
 

next surface

previous surface

2D curves

3D curves

surfaces

fractals

polyhedra

© Robert FERRÉOL  2017