LOXODROMIE DE LA SPHÈRE
Loxodrome
of the sphere, Loxodrome der Kugel
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
LOXODROMIE DE LA SPHÈRE
Loxodrome
of the sphere, Loxodrome der Kugel

| Courbe étudiée par Pedro
Nunes en 1537, Simon
Stevin en 1608, Maupertuis
en 1744; nom donné par Snellius
en 1624.
Autres noms : ligne de rhumb, ligne de vent. |
| En prenant Équation différentielle sphérique : Hormis le cas des parallèles : Équation sphérique : où gd-1 est la fonction de Gudermann inverse, définie pour gd-1 (x) = ln (tan(x/2 + (dont la courbe est la radioïde pseudo-elliptique). Pour Équation sphérique : Équation cylindrique : Abscisse curviligne : Rayon de courbure : Rayon de torsion : |
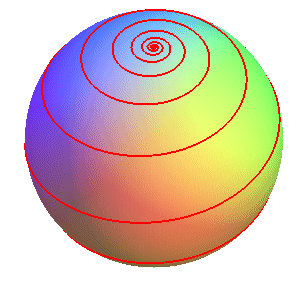
Les loxodromies de la sphère,
associées à un axe donné, sont les courbes faisant
un angle constant avec les parallèles (ou avec les méridiens).
Ne pas confondre les loxodromies avec les hélices
sphériques, qui font, elles, un angle constant avec le plan
de l'équateur, ni avec les clélies.
Les loxodromies correspondent aux droites en coordonnées
de Mercator
; autrement dit, sur les cartes terrestres en projection de Mercator, on
dessine les loxodromies par des droites. L'angle
que font, sur la carte, les images des loxodromies avec l'horizontale est
le même que celui qu'elles font sur la sphère avec les parallèles.
Si l’on connaît les coordonnées géographiques
et
de
deux points, l’angle
associé à la loxodromie la plus courte joignant ces deux
points est obtenu par la formule :
,
et la longueur est donnée par :
.
La notion de loxodromie s'oppose à celle d'orthodromie
(ou géodésique), chemin
le plus court joignant deux points de la sphère, qui est un arc
de grand cercle ; par comparaison, la longueur de
l'orthodromie joignant les deux point ci-dessus est donnée par la
formule .
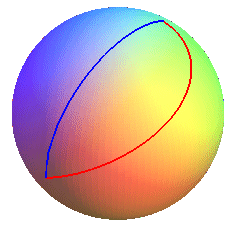 La loxodromie (en rouge) et l'orthodromie (en bleu) joignant le point
de longitude 15° ouest et de latitude 15° sud au point de longitude
150° ouest et de latitude 60° nord.
|
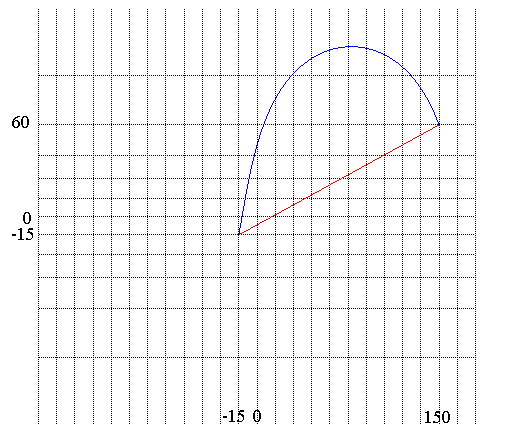
Les mêmes sur une carte en projection de Mercator !!! |
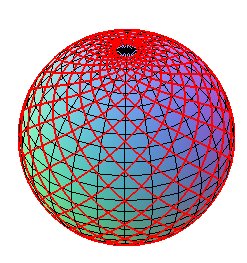
| Le double réseau de loxodromies faisant un angle
de ±45° avec les méridiens forme un élégant
réseau de courbes orthogonales sur la sphère.
Comparer avec le réseau des courbes de Viviani. |
 |
 |
 |
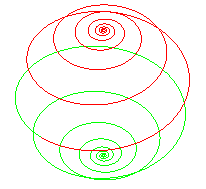
La projection orthogonale de la loxodromie sur le plan
de l'équateur est, comme le montre l'équation cylindrique
ci-dessus, la spirale de
Poinsot bornée : .
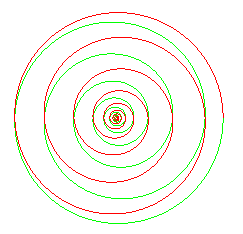
La projection stéréographique de pôle
nord sur le plan de l'équateur est la spirale
logarithmique : ,
faisant le même angle
avec le rayon vecteur que la loxodromie fait avec les méridiens
(puisque la projection stéréographique est une transformation
conforme).
 |
Des loxodromies vues par Escher
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2024