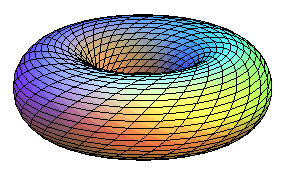
tore ouvert avec ses loxodromies

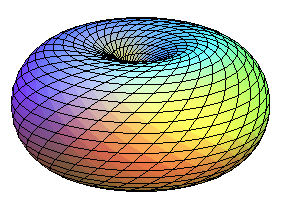
tore à trou nul

tore croisé

 

Voir TPE 96 maths 1

 

1ère méthode, en coordonnées toriques. Équation différentielle : , pour le tore , étant l'angle que font les loxodromies avec les parallèles. Pour le tore ouvert (a > b) : . La courbe est rationnelle (et est alors fermée) pour  rationnel, et lorsque m = 1, soit pour  ou encore , on obtient les cercles de Villarceau. Pour le tore à trou nul (a = b) : . Pour le tore croisé (a < b) : . 2ème méthode en coordonnées cylindriques. Équation différentielle : , pour le tore . Pour le tore ouvert (a > b) :  (, ) ; les projections sur xOy sont donc des polygastéroïdes. Pour le tore à trou nul (a = b) :  (inverse de spirale de Galilée). Pour le tore croisé (a < b) :  avec ,.

 

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL  2014