Équation cylindrique :  (avec  a = rayon majeur, b = rayon mineur) Paramétrisation torique : . Paramétrisation cartésienne où les lignes de coordonnées sont les cercles méridiens et les cercles parallèles : . Paramétrisation cartésienne où les lignes de coordonnées sont les cercles de Villarceau et les cercles parallèles, dans le cas a > b  ( pour une famille de cercles, –1 pour l'autre) :  Équation cartésienne :  soit . Surface quartique.rationnelle. Avec la première paramétrisation : Première forme quadratique fondamentale : . Élément d’aire : . Deuxième forme quadratique fondamentale : . Courbure de Gauss : . Courbure moyenne : . Volume et aire pour .   Autre paramétrisation pour le tore à trou nul : avec  pour la partie externe,  pour la partie interne.

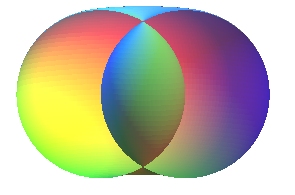
Le tore est la surface engendrée par la révolution d'un cercle (C) autour d'une droite (D) de son plan ; c'est donc un tube de diamètre constant et d'âme un cercle.
Ici (D) est l'axe Oz, b (rayon mineur du tore) le rayon de (C) et a (rayon majeur du tore) la distance de son centre à (D).
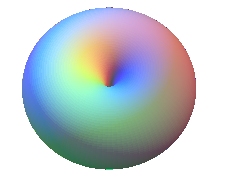
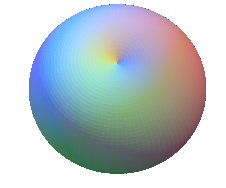
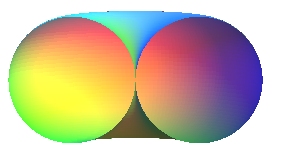
Si (D) est sécante au cercle (), on obtient un tore croisé, fermé, ou rentrant, en forme de citrouille ou de cerise (en anglais  "spindle torus") avec pour cas limites la sphère si (D) est un diamètre (a = 0), et le tore à collier nul ou à trou nul (en anglais "horn torus") si (D) est tangente au cercle (a = b).
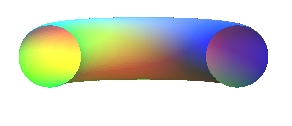
Sinon (cas habituel a > b) on obtient un tore à trou, à collier, à gorge, ou encore ouvert , en forme de chambre à air (en anglais "ring torus").
 

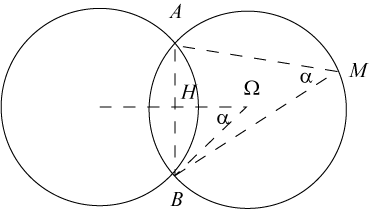
Dans le cas croisé , le tore possède deux point singuliers A et B, points d'intersection communs aux cercles générateurs. D'après le théorème de l'angle inscrit, il peut donc être vu comme le lieu des points M d'où l'on voit le segment [AB] sous un angle constant  (surface isoptique). Dans la figure ci-contre,  et , donc  et .

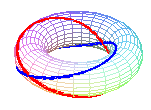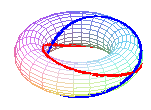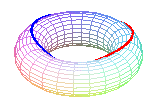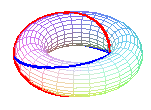
Le tore est une surface quadruplement cerclée : hormis les méridiennes (sections par les plans passant par l'axe de révolution) et les parallèles (sections par les plans orthogonaux à l'axe), il existe deux famille de cercles obtenus par les sections par les plans bitangents au tore, appelés cercles de Villarceau :
 

La bande située entre deux cercles de Villarceau voisins ressemble à un ruban de Möbius mais n'en est pas un puisqu'elle a deux bords. Sa torsion est d'un tour.

Les courbes tracés sur un tore sont les spiriques (ou courbes toriques).
Regarder en particulier les sections planes, les géodésiques, les asymptotiques et les loxodromies du tore.

Pour le contour de la projection d'un tore, voir à toroïde.
Les surfaces inverses du tore sont les cyclides de Dupin.
Pour un tore particulier minimisant l'énergie de courbure, voir à tore de Wilmore.

Pour le tore en tant que notion topologique, voir l'entrée suivante.

Voir aussi le dôme de Bohème, le tore de Clifford, et les tores sinusoïdaux.

Les américains surnomment le tore : donut, du nom de la pâtisserie ci-dessus, mais en cuisine il y a d'autres tores comme les onion rings...	De nombreux fruits ont la forme (très approchée) de la partie interne d'un tore croisé (ci-dessus, le fruit du cacaoyer). Pour la partie externe, penser à une tomate.	Ces voûtes en éventail ont la forme de parties internes de tores à trou nul.

Une poulie est un  demi-tore

 

surface suivante

surface précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL 2020