Géodésique du tore

GÉODÉSIQUE DU TORE
Torus Geodesic, Geodätische des Torus

Pour le tore

:
Système différentiel :

.
En posant

, équation différentielle :

, où c est une constante.

La résolution de l'équation différentielle ci-dessus conduit à des intégrales elliptiques.

Les géodésiques sont soit enroulées, soit non enroulées ; même lorsqu'elle le sont, ce ne sont pas des solénoïdes toriques (sauf dans les cas limites des méridiennes et des 2 cercles de gorge).

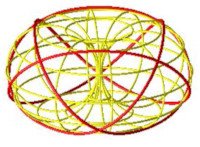
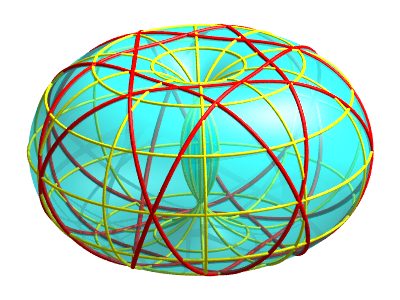
Géodésiques enroulées fermées, à symétries d'ordre 3, 4
et 6.

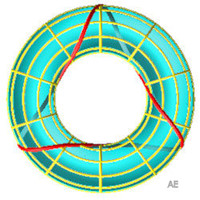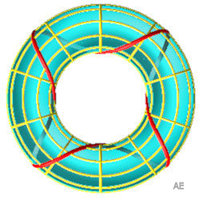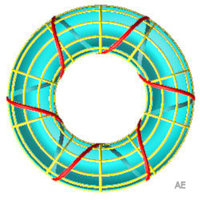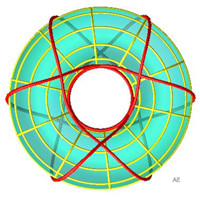
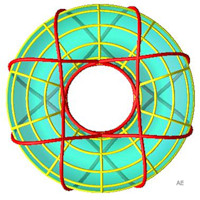
Géodésiques non enroulées fermées, à symétries d'ordre 3, 3
et 4, et respectivement 9, 12 et 16 croisements.

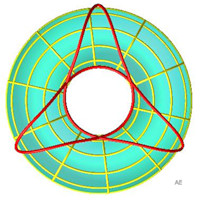
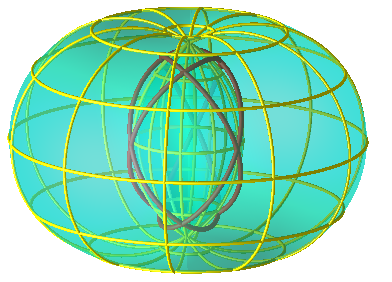Géodésique fermée non enroulée du tore à trou nul, symétrie d'ordre 4 (correspondant au noeud 8.18). Géodésique fermée non enroulée du tore croisé, symétrie d'ordre 7. Idem sur la partie interne, symétrie d'ordre 3 (correspondant au noeud 9.40)

Voir aussi les asymptotiques du tore, ainsi que les géodésiques de l'ellipsoïde de révolution.

courbe suivante courbe précédente courbes 2D courbes 3D surfaces fractals polyèdres

Géodésiques enroulées fermées, à symétries d'ordre 3, 4 et 6.
Géodésiques non enroulées fermées, à symétries d'ordre 3, 3 et 4, et respectivement 9, 12 et 16 croisements.


Géodésique fermée non enroulée du tore à trou nul, symétrie d'ordre 4 (correspondant au noeud 8.18).	Géodésique fermée non enroulée du tore croisé, symétrie d'ordre 7.	Idem sur la partie interne, symétrie d'ordre 3 (correspondant au noeud 9.40)