Spirale de Galilée

SPIRALE DE GALILÉE
Galilean spiral, Galileische Spirale

Courbe étudiée par Fermat en 1636.
Galilée (1564-1642) : physicien et astronome italien.

Équation polaire réduite :

.
Abscisse curviligne :

(rectification algébrique si a = 0, elliptique sinon).
Rayon de courbure pour a = 0 :

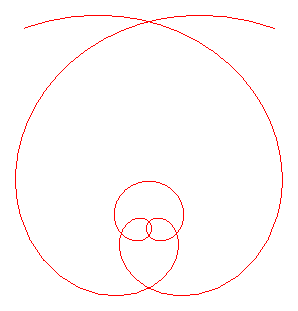
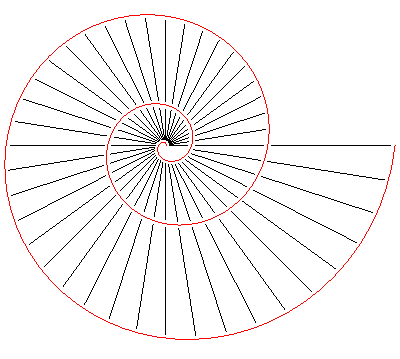
La spirale de Galilée est la trajectoire d'un point se déplaçant d'un mouvement uniformément accéléré sur une droite d’un plan, cette droite tournant, elle, uniformément autour d'un de ses points.

L'équation polaire générale d'un tel mouvement est donnée, avec les notations cinématiques classiques, par :

qui après rotation donne bien une équation polaire du type ci-dessus.

Comme

, on peut considérer que la spirale est le bord d'une bande trapézoïdale enroulée. Et n'y a-t-il pas une ressemblance avec la queue du caméléon ?

La trajectoire d'un corps soumis à la pesanteur (en négligeant les frottements, et sur une portion petite par rapport à la distance au centre de la terre) dans le plan de l'équateur rapporté à un référentiel terrestre est une portion de spirale de Galilée.
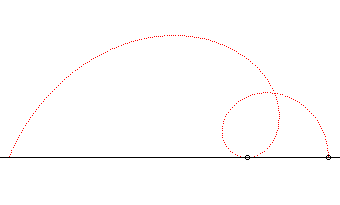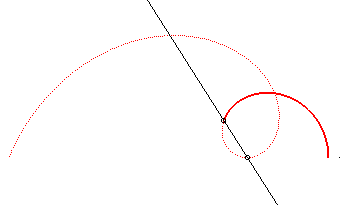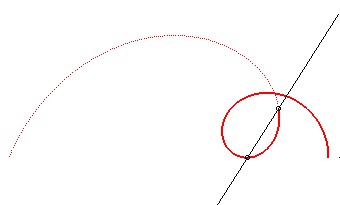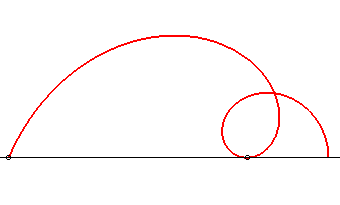
Galilée avait posé le problème de cette trajectoire, sous forme de recherche de la courbe suivie par une pierre tombant d'une tour, d'où le nom donné à cette spirale.
Il pensait que cette trajectoire était très probablement un arc de cercle. Il se trompait de peu comme le montre la portion de spirale

ci-contre !
L'aire de la boucle de spirale vaut

et celle du disque

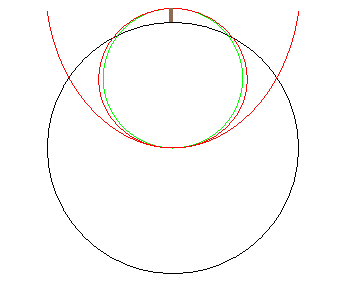
En noir, la terre, en rouge, la spirale de Gallilée,
approchée par le cercle vert.

La spirale de Galilée ne présente un rebroussement en O que pour a =0

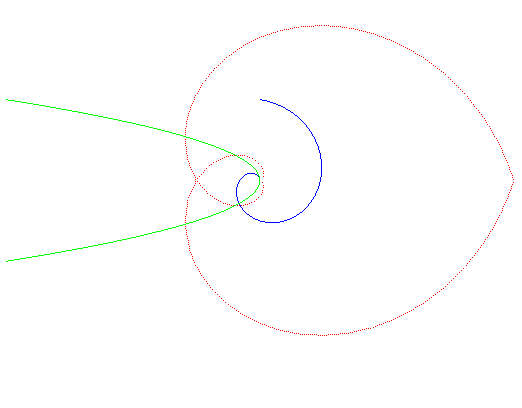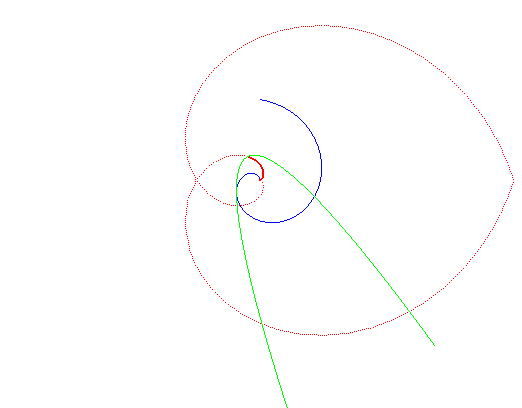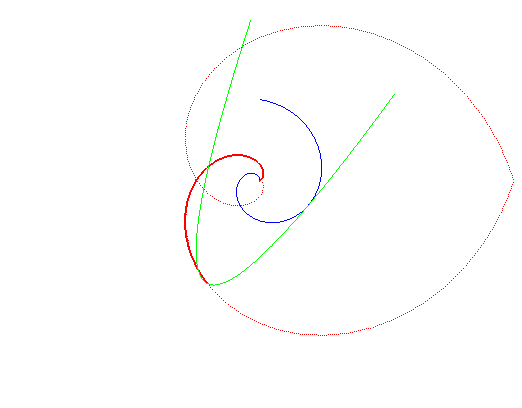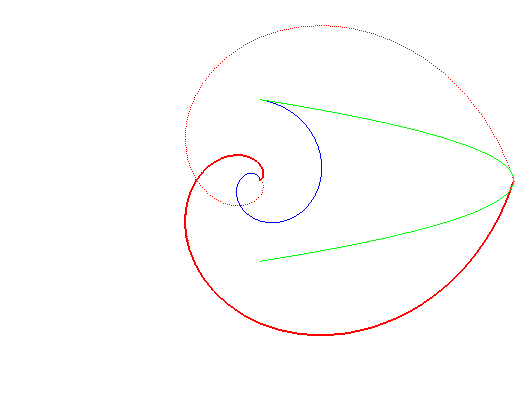Elle s'obtient comme roulette du mouvement associé
au roulement d'une parabole sur une spirale d'Archimède.

La spirale de Galilée est aussi un cas particulier de courbe isochrone de Varignon.

Dans le cas a = 0, on a quand tend vers l'infini : la spirale de Galilée est proche de la spirale de Sturm, qui vérifie, elle, exactement .

courbe suivante courbe précédente courbes 2D courbes 3D surfaces fractals polyèdres