La spirale de Norwich est la courbe, autre qu'un cercle, telle que le rayon de courbure est en tout point égal à la distance à un point fixe (d'où le nom de radioïde aux cordes). C'est donc un cas particulier de spirale de Sturm.
 

Équation différentielle :  (p est le rayon podaire). Intégrale première : , le cas a = 0 donne le cercle, mais, dans le cas a > 0, on obtient : Équation polaire : , paramétrisation polaire : . Abscisse curviligne : , angle tangentiel polaire : . Rayon podaire : , rayon de courbure : . Équation intrinsèque 1 : .

 
 

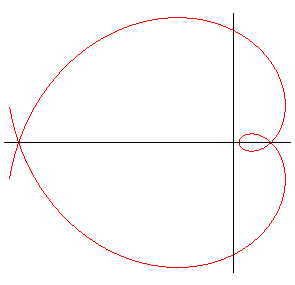A droite, figure illustrant le fait que tout point de la spirale de Norwich (en rouge) est à même distance du centre de courbure que de O. En bleu, la développée, lieu des centres de courbure.

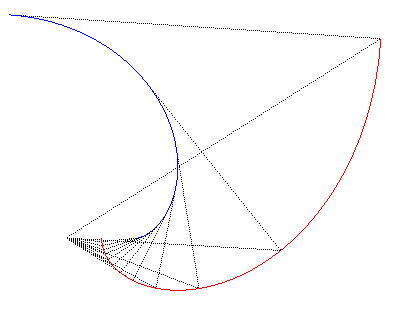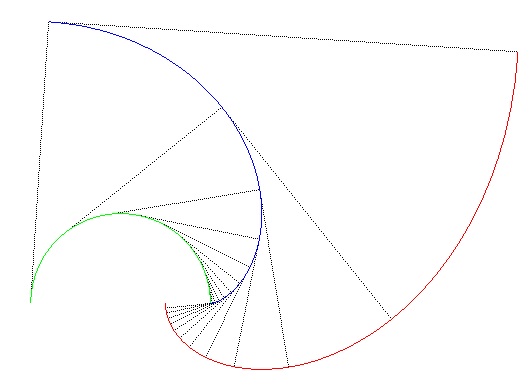
Or on s'aperçoit, en déterminant par exemple son équation intrinsèque, que cette développée n'est autre qu'une développante de cercle (plus précisément du cercle de centre O et de rayon 2a). La spirale de Norwich est donc l'une des développantes secondes de cercle. Et les développantes secondes de cercle sont les courbes telles que le rayon de courbure est en tout point égal à la distance au centre du cercle, plus une constante. On peut caractériser la spirale de Norwich parmi ces développantes secondes par le fait qu'elle coupe orthogonalement le cercle.

 
 
 

La spirale de Norwich est l'antipodaire de la spirale de Galilée : ,
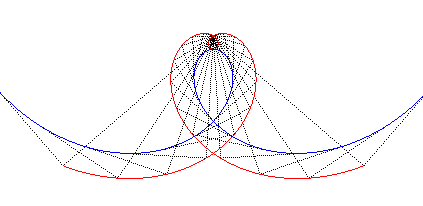et elle est asymptote à la spirale de Galilée :.

Voir aussi les liens entre la spirale de Norwich et la cubique de Tschirnhausen, ainsi que la spirale de Norwich inverse.
 
 

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL  2015