Cubique de Tschirnhausen

CUBIQUE DE TSCHIRNHAUSEN
Tschirnhausen cubic, Tschirnhausensche Kubik

Courbe étudiée par Tschirnhaus en 1690, L'Hospital en 1696 et Catalan en 1832.
Nom donné en 1900 par R C Archibald, en rajoutant "en" à la fin du nom de Tschirnhaus.
Autres noms : trisectrice de Catalan, cubique de L'Hospital, orthogénide [?loria].
Ehrenfried von Tschirnhaus (1651-1708) : physicien et géomètre allemand.

	Dans (O, , ) : Équation cartésienne : . Paramétrisation cartésienne : . Cubique polynomiale à point double. Le sommet est A(9a, 0) et le point double O. Autre paramétrisation cartésienne partielle (en gras ci-contre) :
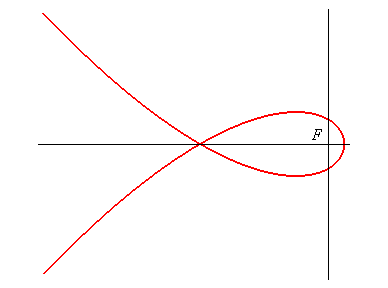	Équation cartésienne dans (F, , ) (où F(8a, 0) est le foyer de la parabole podaire, d'équation , et p = 2a son paramètre) : Équation polaire : . Paramétrisation cartésienne : ( t = tan(q/3)). Abscisse curviligne donnée par ou . Aire de la boucle : .

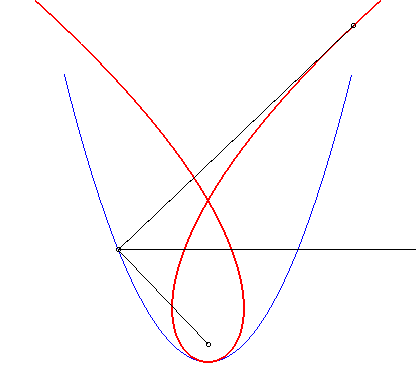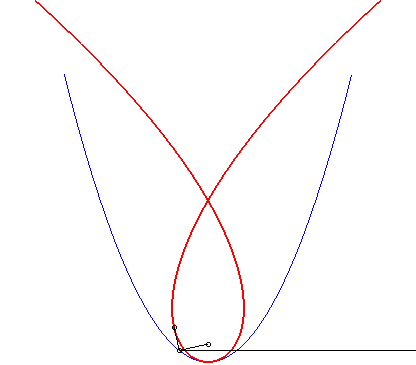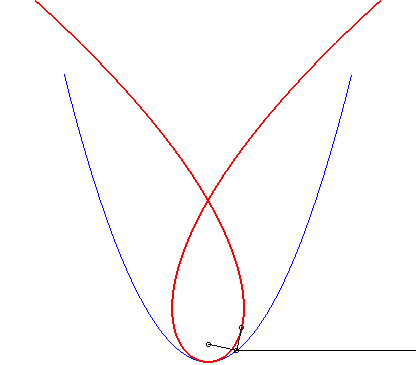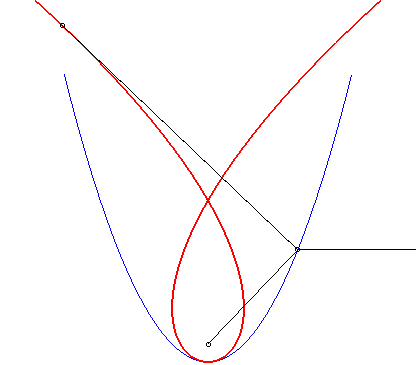
La cubique de Tschirnhausen est l’antipodaire de la parabole par rapport à son foyer F, et la caustique par réflexion de cette même parabole pour des rayons lumineux perpendiculaires à l'axe de la parabole (ces deux propriétés étant liées, grâce à la propriété de la tangente à la parabole). On montre même que la caustique par réflexion de la parabole est une cubique de Tschirnhausen quelle que soit la direction des rayons, sauf lorsqu'ils sont parallèles à l'axe de la parabole auquel cas on obtient le foyer.
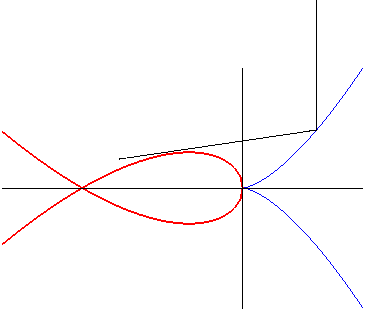
La cubique de Tschirnhausen est aussi caustique par réflexion de la parabole semi-cubique pour des rayons perpendiculaires à son axe.
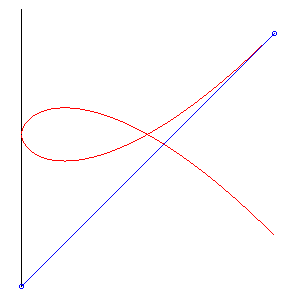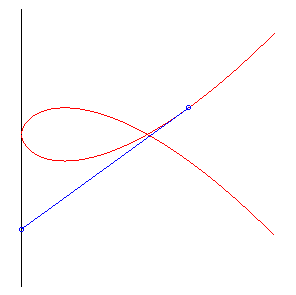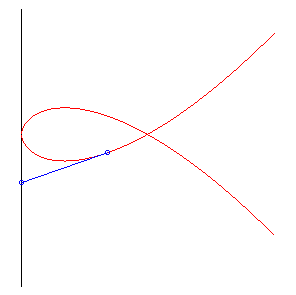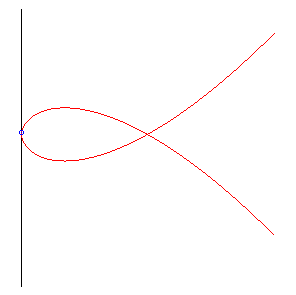
Elle est donc aussi la courbe suivie par un chien cherchant à rattraper son maître avec une vitesse double de lui.
Elle est aussi, à dilatation près, la projection de la parabole gauche : sur le plan x+z = 0.
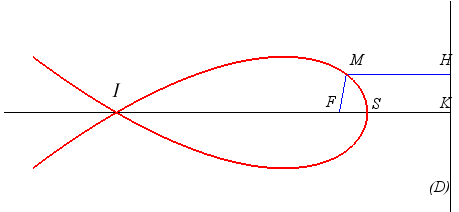
Si (D) est la droite perpendiculaire à l'axe de symétrie, de pied K défini par , la cubique de Tschirnhausen est le lieu des points M vérifiant; par analogie avec les coniques, la droite (D) sera appelée la directrice de la cubique et F le foyer.

L’équation cartésienne montre que la cubique de Tschirnhausen est un cas particulier de parabole divergente et l’équation polaire que c’est un cas particulier de spirale sinusoïdale.

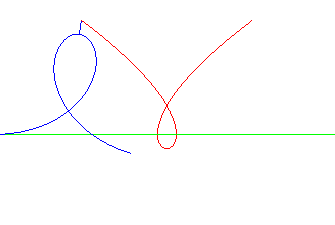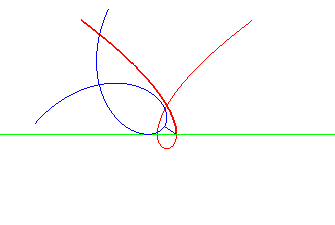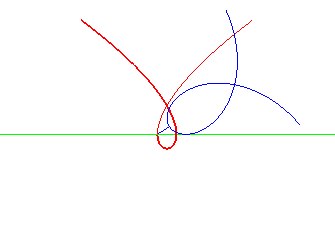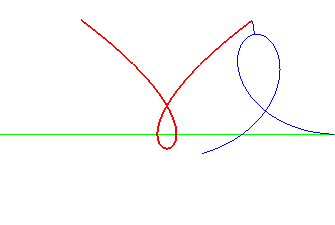
La cubique de Tschirnhausen est la roulette du pôle d'une spirale de Norwich roulant sur une droite. La droite est alors la normale double à la cubique.

On en déduit, d'après un théorème de Mannheim, que la cubique de Tschirnhausen est la courbe suivie par un crabe marchant à même vitesse qu'un mobile rectiligne, et face à lui (voir à courbe de Duporcq).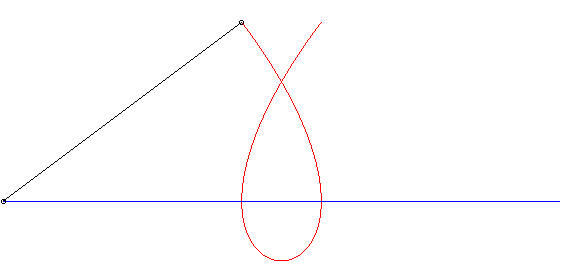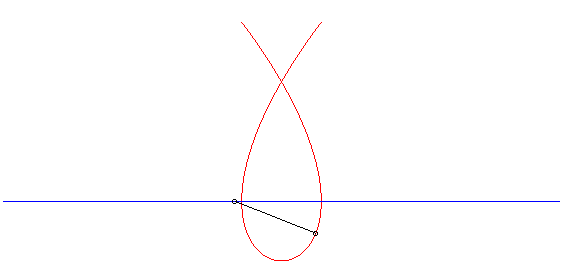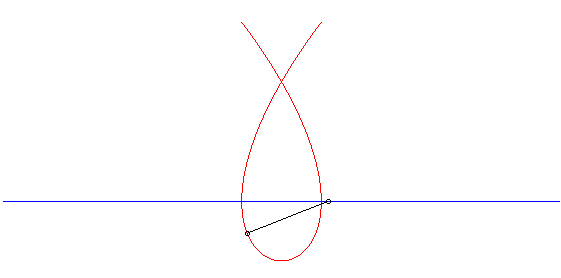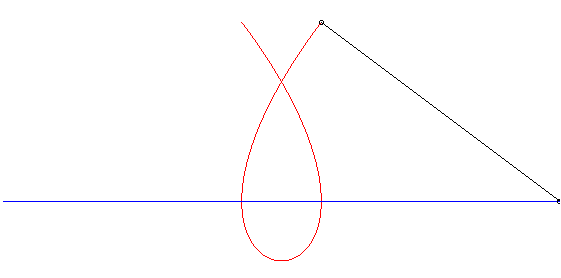

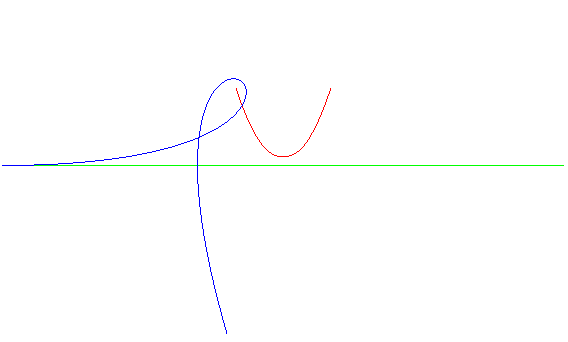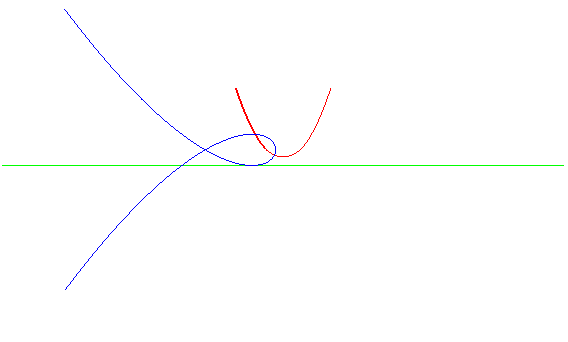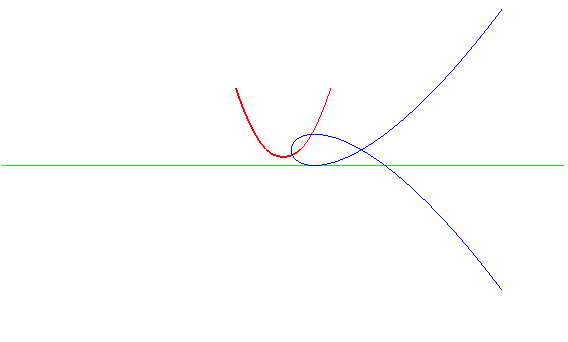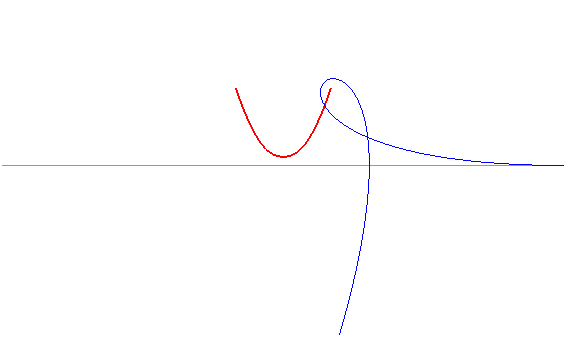
Et inversement, la roulette du foyer d'une cubique de Tschirnhausen roulant sur une droite est une parabole.
La glissette de ce même foyer est une cubique duplicatrice.

Christophe Masurel a cherché les "roues" qui, roulant sur une cubique de Tschirnhausen, ont un moyeu ayant une trajectoire rectiligne (voir à couple roue/route) ; partant de la route de Tschirnhausen, on obtient la roue , dont trois cas donnent des courbes remarquables :
k = 1 : la roue est une spirale de Galilée (figure de gauche), et la trajectoire du pôle est la normale double à la cubique.
k = –1 : la roue est une spirale de Norwich et la trajectoire du pôle est la directrice de la cubique.
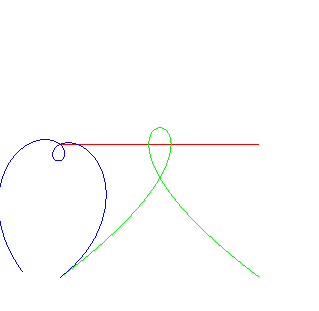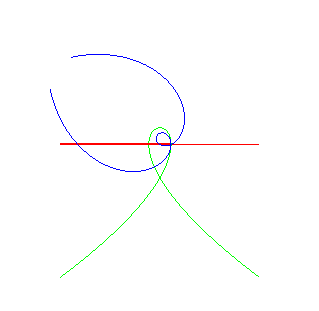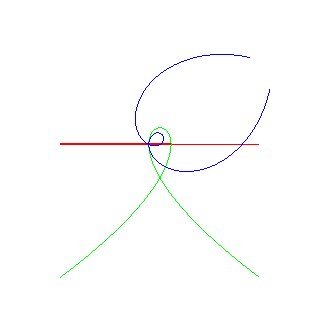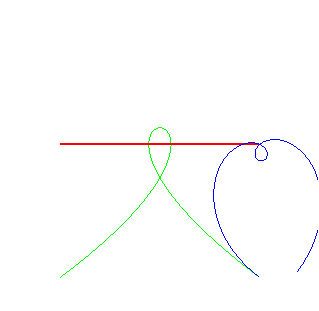
k = 0 la roue : soit est une spirale anallagmatique.
La roulante est une spirale de Galilée,
et la roulette la normale double.
Dans ce cas la courbe associée au
théorème de Steiner Habich est une spirale de Norwich.

La roulante est une spirale de Norwich
et la roulette la directrice.

Lorsqu'une cubique de Tschirnhausen roule sur une droite, sa directrice enveloppe une cubique de Tschirnhausen égale dont la normale double est la droite de roulement.
Ceci vient du théorème : dans un couple roue/route, si on fait rouler la route sur une droite, l'axe décrit par le moyeu de la roue associée à cette route enveloppe une courbe qui est la roulette rectiligne du moyeu de la roue ; ici la route est une cubique de Tschirnhausen, l'axe sa directrice, et la roue une spirale de Norwich. Comme il se trouve que la roulette rectiligne de la spirale de Norwich est une cubique de Tschirnhausen, on obtient la propriété.

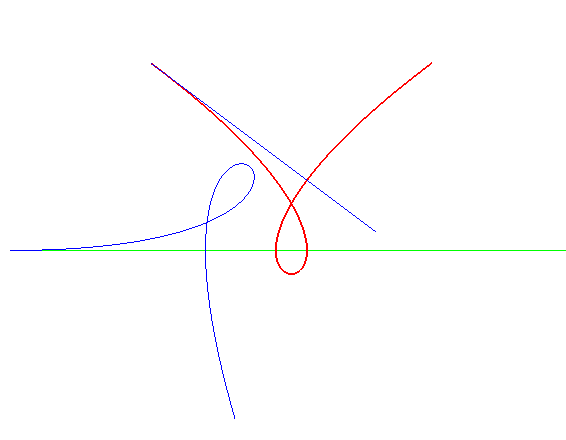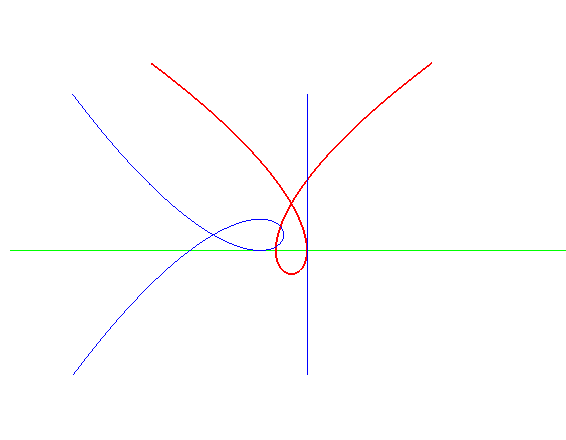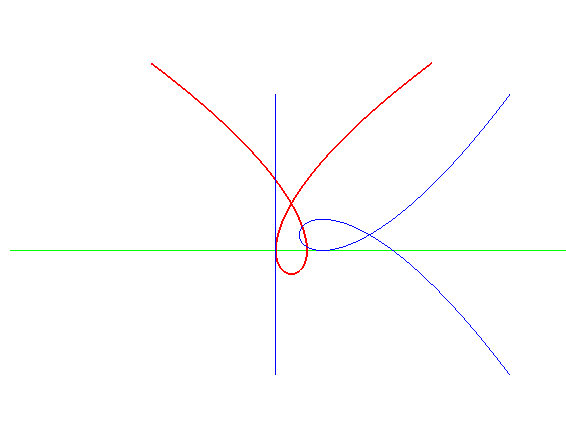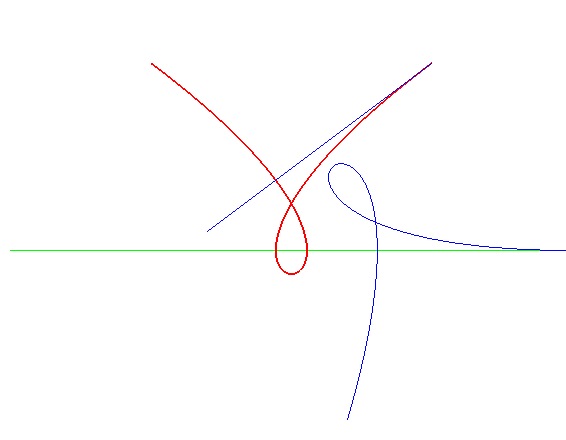La cubique de Tschirnhausen est une trisectrice (voir Brocard Lemoyne III p.140).

La surface d'Enneper est la surface minimale contenant la cubique de Tschirnhausen comme géodésique.

La cubique de Tschirnhausen, qui est aussi celle de L'Hospital, n'est pas à confondre avec la quintique de ce dernier.

courbe suivante courbe précédente courbes 2D courbes 3D surfaces fractals polyèdres

La cubique de Tschirnhausen est la roulette du pôle d'une spirale de Norwich roulant sur une droite. La droite est alors la normale double à la cubique.
On en déduit, d'après un théorème de Mannheim, que la cubique de Tschirnhausen est la courbe suivie par un crabe marchant à même vitesse qu'un mobile rectiligne, et face à lui (voir à courbe de Duporcq).
Et inversement, la roulette du foyer d'une cubique de Tschirnhausen roulant sur une droite est une parabole. La glissette de ce même foyer est une cubique duplicatrice.