quelconque. Le cas le plus célèbre est le cas n =
3, puisque non résoluble à la règle et au compas ;
les courbes correspondantes sont dénommées trisectrices
(remarquer
que bissectrice possède deux s, tandis que trisectrice n’en a qu’un...).
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
(COURBE) SECTRICE
Sectrix
curve, Sektrix
Une sectrice est une courbe auxiliaire permettant
de résoudre graphiquement le problème de la section d'un
angle en n angles égaux avec n naturel
quelconque. Le cas le plus célèbre est le cas n =
3, puisque non résoluble à la règle et au compas ;
les courbes correspondantes sont dénommées trisectrices
(remarquer
que bissectrice possède deux s, tandis que trisectrice n’en a qu’un...).
Exemples de familles de courbes n- sectrices :
- les sectrices
de Maclaurin
- les sectrices
de Ceva.
- les sectrices
de Delanges.
Exemples de courbes n - sectrices pour tout n
:
- la spirale
d'Archimède
- la quadratrice
de Dinostrate.
Exemples de trisectrices :
- la conchoïde
de Nicomède
- la trisectrice
de Maclaurin
- la cubique
de Tschirnhausen (ou trisectrice de Catalan)
- le limaçon
trisecteur
- le trèfle
équilatère (ou trisectrice de Longchamps)
- la trisectrice
de Ceva
- la trisectrice
de Delanges
- le folium
de Dürer
- l'hyperbole
d'excentricité 2.
| Quatre des neuf trisectrices précédentes
peuvent être définies à partir de la figure ci-contre,
attribuée à Archimède, renfermant un angle et son
triple.
Dans les 2 constructions suivantes, la longueur L est
fixée.
Si l'on fixe A et (D), et que (D') pivote autour de A, C coulissant sur (D), le point D décrit la trisectrice de Ceva, de pôle A (et la droite (BC) enveloppe une astroïde). Si l'on fixe C et D, et que (D) pivote autour de C, (D') pivote autour de D, B coulissant sur (D') décrit un cercle de centre C, mais surtout, A décrit le limaçon trisecteur, de pôle D. Dans les 3 constructions suivantes la longueur L est variable. Si l'on fixe A et C, et que (D') pivote autour de A, B décrit la médiatrice de [AC], mais surtout, D décrit la trisectrice de Maclaurin, de pôle A. Si l'on fixe A et D, et que (D) pivote autour de A, B coulissant sur (D'), C décrit une hyperbole d'excentricité 2. Une cinquième possibilité, explorée
par Geneviève Tulloue, est de fixer D et (D), de faire pivoter (D')
autour de D, A et C coulissant sur (D). Le point B décrit alors
une courbe d'équation polaire |
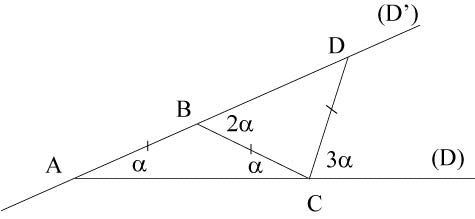
AB = BC = CD=L |
Animation de la construction de la trisectrice de Ceva par cette méthode (animations réalisées avec cabri par Geneviève Tulloue)
Animation de la construction du limaçon trisecteur par cette méthode :
Animation de la construction de la trisectrice de Maclaurin par cette méthode :
Animation de la construction de l'hyperbole d'excentricité 2 par cette méthode :
Animation de la construction de la trisectrice de Tulloue par cette méthode :
Lien en néerlandais sur les trisectrices : www.pandd.demon.nl/trisect.htm#top
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2013
,
que l'on peut donc appeler "trisectrice de Tulloue".