FOLIUM DE DÜRER
Durer's
folium, Durersches Blatt
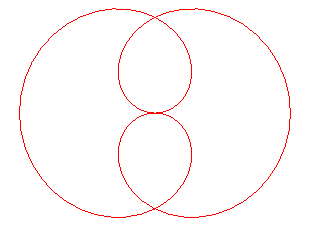
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
FOLIUM DE DÜRER
Durer's
folium, Durersches Blatt
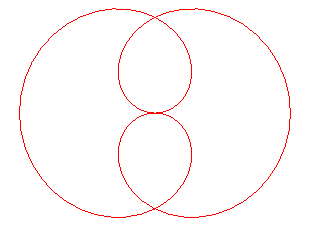
| Albrecht Dürer (1471 - 1528) : peintre et graveur allemand. |
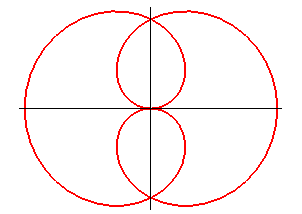 |
Équation polaire : Paramétrisation cartésienne : Équation cartésienne : Sextique: rationnelle. |
Le folium de Dürer est un cas particulier de rosace, pour n = 1/2 ; c'est donc aussi un cas particulier d'épitrochoïde, avec q = 2 et k = 3.
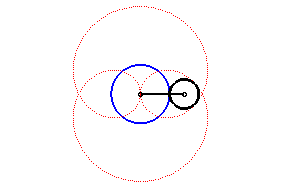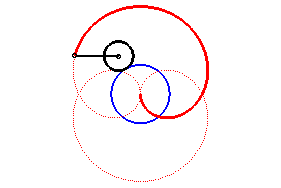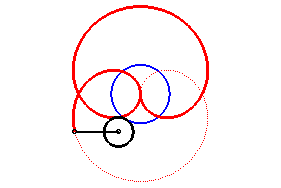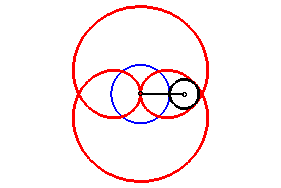
| Il est aussi l'inverse de la trisectrice de Delanges, et possède donc lui aussi une propriété de trisection, indiquée ci-contre ; l'angle MOP est le tiers de AOP. | 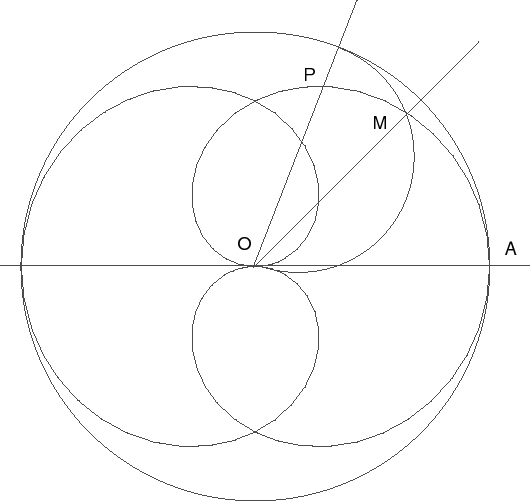 |
Voir aussi la néphroïde de Freeth qui est une de ses conchoïdes.

Folium de Dürer réalisé avec une courroie
d'engrenage par Lévi Caparéda.
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2020