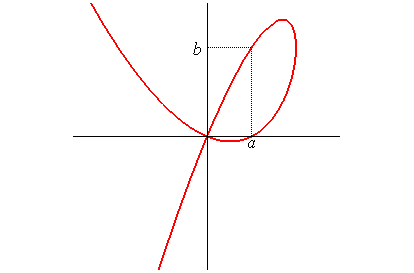Équation cartésienne : . Équation polaire : . Cubique rationnelle à point double.

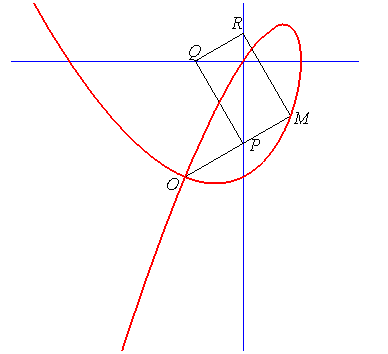
Un point O et deux droites (D₁) et (D₂) perpendiculaires étant données (ici, les droites x = a  et y = b), une droite variable (D) passant par O rencontre (D₁) en P ; la perpendiculaire en P rencontre (D₂) en Q ; la perpendiculaire en Q rencontre (D₂) en R ; la perpendiculaire en R rencontre (D) en M : le folium parabolique (qui n'est pas un folium) est le lieu de M.

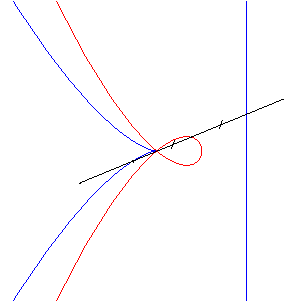
Le folium parabolique est dit droit lorsque D2 passe par O (b = 0), auquel cas il est symétrique par rapport à (D2). C'est alors un cas particulier de parabole divergente et de larme. Son équation mise sous la forme  montre que c'est la cissoïdale d'une droite et d'une parabole semi-cubique.

© Robert FERRÉOL, Jacques MANDONNET 2001