Courbe étudiée par Longchamps en 1884, Brocard en 1887. Du latin folium : "feuille".

 

Équation polaire : . Équation cartésienne : . Quartique rationnelle.

Les foliums sont les podaires de deltoïde ; ici, le point O est le pôle de la podaire, et la deltoïde est de centre A(a, b) et de point de rebroussement B(a – 3r, b) ; r est le rayon du cercle inscrit dans la deltoïde, qui a pour paramétrisation : .

Lorsque le pôle de la podaire est situé sur la deltoïde, on obtient les bifoliums ; plus précisément, si l'on pose  on obtient le bifolium : .
Lorsque le pôle de la podaire est situé à l'intérieur de la deltoïde, on obtient les trifoliums.

Pour b = 0 (cas où le pôle de la podaire est situé sur un axe de la deltoïde), le folium est dit droit (il est alors symétrique par rapport à Ox), sinon, oblique.

Cas particuliers de foliums droits :
a = – r (pôle de la podaire en un sommet de la deltoïde): bifolium régulier.
a = 0 (pôle de la podaire au centre de la deltoïde) : trifolium régulier (rosace à trois pétales).
a = r : torpille (équation polaire ).
a = 3r (le pôle de la podaire est en un point de rebroussement de la deltoïde): folium simple.
Pour , le folium prend une belle forme d'oeuf : 
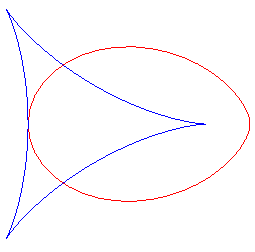
Voir aussi les scarabées, qui sont à l'astroïde ce que sont les foliums à la deltoïde.

Les foliums de Descartes, paraboliques, et de Dürer ne sont pas des foliums au sens de cette page.
 
 

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL  2015