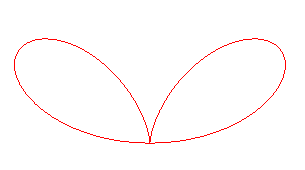
BIFOLIUM RÉGULIER (OU DROIT)
Regular
bifolium, regelmässiges Zweiblatt
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
BIFOLIUM RÉGULIER (OU DROIT)
Regular
bifolium, regelmässiges Zweiblatt

| Origine : voir à bifolium. |
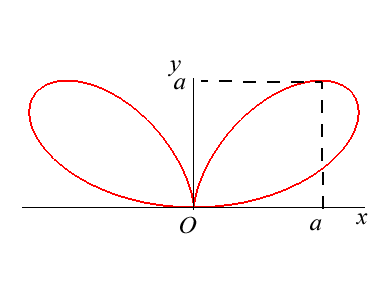 |
Équation polaire : (ou Équation cartésienne : Paramétrisations cartésiennes : Aire totale : Quartique circulaire rationnelle. |
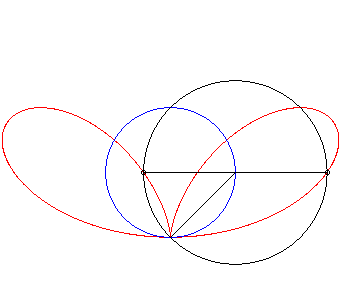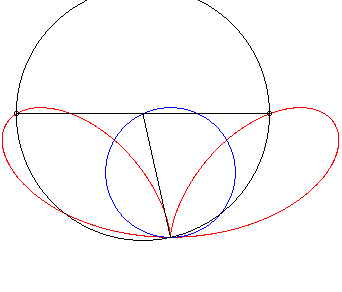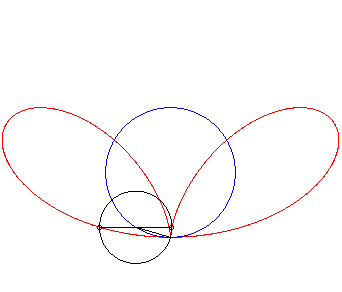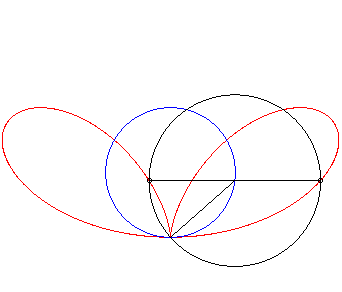
| Étant donné un point variable N
d'un cercle de diamètre [OA] (ici A(0,a)),
le bifolium régulier est le lieu des points M de la perpendiculaire
à (OA) passant par N tels que NM = ON.
Autrement dit, le bifolium régulier est une courbe strophoïdale de cercle, pour un pôle O situé sur le cercle, et un point A à l'infini dans la direction de la tangente en O au cercle. |
 |
| L'équation cartésienne |
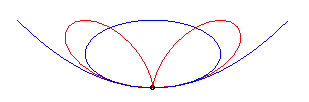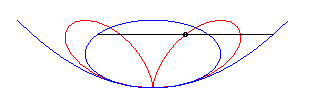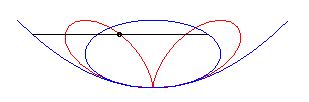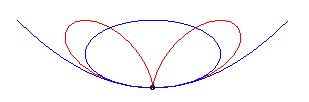 |
| Le bifolium régulier aussi est la podaire de la deltoïde par rapport à un de ses sommet (voir à folium). |
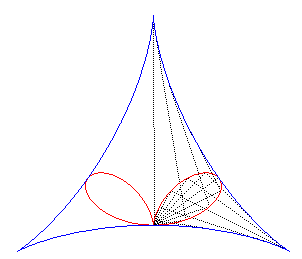 |
| C'est aussi une projection plane de la courbe de Viviani. |  |
Il s'obtient aussi comme orthopolaire de cercle.
Voir aussi les poissons
et comparer avec le double-coeur
et la podaire de la tractrice.
| Une variante : |
Une autre : |
Rajouter un |
Plus généralement, donne un n-folium. |
 |
 |
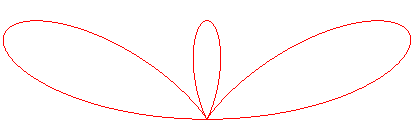 |
 |
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL, Jacques MANDONNET 2017