Équation cartésienne :  , soit  où P et Q sont des polynômes de degré  2 ;  Quartique (de genre 1) à axe de symétrie.

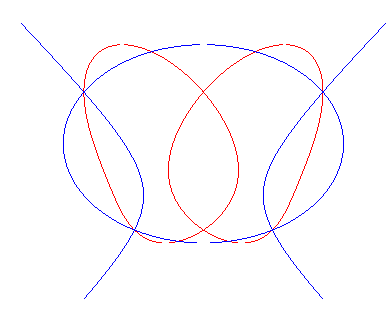
Les courbes polyzomales sont les courbes médianes de deux coniques ayant un axe en commun, parallèlement à une perpendiculaire à cet axe ; en effet, en écrivant l'équation ci-dessus sous la forme  , on voit qu'elle représente la courbe médiane des deux coniques d'axe Ox :   et .

Les courbes polyzomales recouvrent toutes les quartiques à axe de symétrie ayant un ou deux points doubles sur l'axe (éventuellement imaginaires) (??).

Ruiz-Castizo a montré qu'on pouvait générer ces courbes à partir d'une conique (C) et d'une droite (D) en faisant coulisser un segment de longueur constante [PQ], P étant astreint à rester sur la conique (C) et Q sur la droite (D) et en considérant le lieu d'un point M fixe sur la droite (PQ) (voir [Gomes Texeira T2] page 308) ; lorsque la conique (C) est un cercle, on obtient en particulier les courbes de la bielle de Bérard.

Lorsque les deux coniques sont des cercles tangents, on obtient les doubles-cœurs et lorsque les coniques  et  sont l'une une parabole, l'autre le cercle osculateur au sommet de la parabole, on obtient le bifolium régulier.

Lorsque les deux coniques sont des cercles concentriques, on obtient les quartiques de Bernoulli.

Lorsque les deux coniques sont des paraboles orientées en sens contraires, on obtient les besaces (dont la lemniscate de Gerono quand les paraboles sont isométriques).

En fait, la définition des courbes polyzomales par Cayley est beaucoup plus générale ; il s'agit des courbes algébriques ayant une équation pouvant se mettre sous la forme où les U_i sont des polynômes de degré maximum m ; la courbe est alors de degré  ; chaque courbe U_i(x,y) = 0 est une zomale ou ceinture de la courbe. Cayley a montré que les trizomales avec m = 2 sont exactement les quartiques ; il s'agit ci-dessus d'un sous-cas.
 

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL  2008