Courbe étudiée par le Marquis de L'Hospital qui a publié dans les Acta  Eruditorum en 1695 cette magnifique planche. Le système a été mis en pratique pour les pont-levis par l'ingénieur Bernard Forest de Bélidor, pont-levis qui depuis portent son nom (cf. dictionnaire portatif de l'ingénieur 1755). Il a désigné ce système : pont-levis à sinusoïde, bien que la courbe ne soit pas une sinusoïde au sens actuel. Courbe étudiée par Poncelet en 1845.

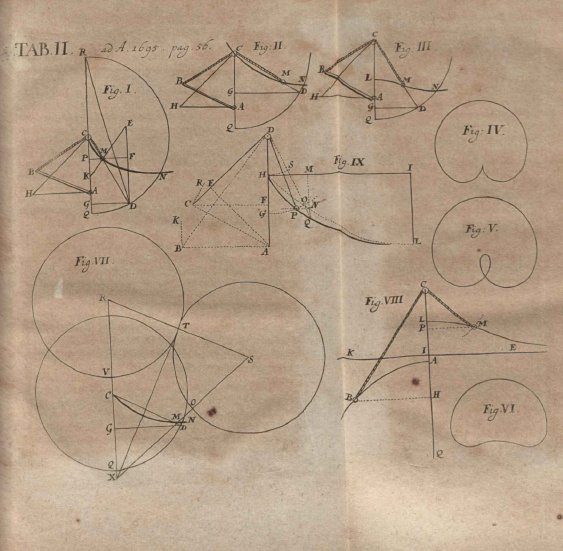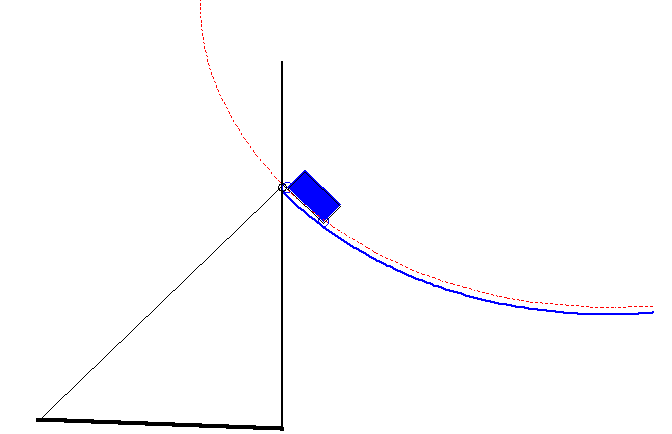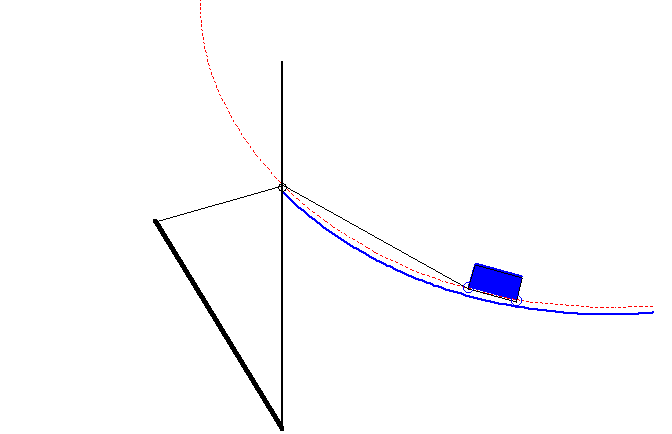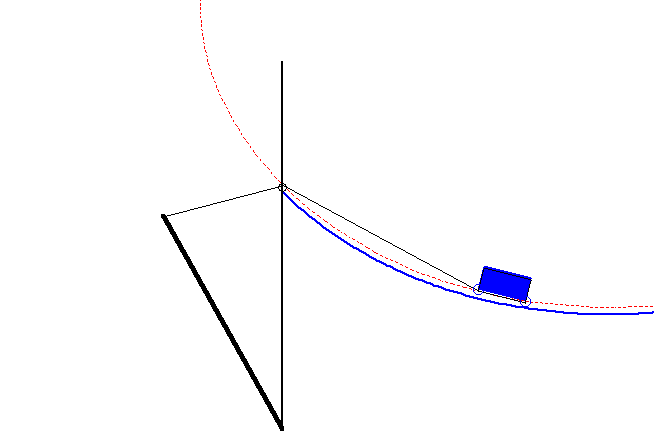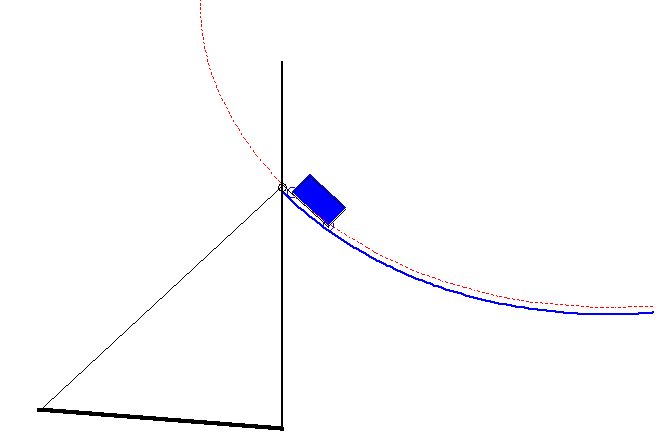
La courbe du pont-levis est la courbe décrite par l'extrémité du contre-poids d'un pont-levis (cf figure ci-dessus) de sorte que le système pont + contre-poids soit constamment en équilibre.

On montre que cette courbe n'est autre qu'une portion d'ovale de Descartes.

Voici une démonstration de ce fait :

Avec les notations de la figure ci-contre, écrivons que l'énergie potentielle totale est constante :  ; en éliminant  entre cette relation et la relation d'Al-Kashi : , on obtient  dont on peut montrer que c'est l'équation d'un ovale de Descartes dont un foyer est situé à 2hQ/p de C. L'ovale se réduit au limaçon de Pascal : si . Si l'on considère le cas où le contre-poids est en C lorsque le pont est baissé, alors la constante E est nulle et  ; la courbe du pont-levis est alors toujours le limaçon de Pascal , qui sera une cardioïde si . Dans le cas général, si  et  quand le pont est baissé, alors  et l'ovale est un limaçon si  ou .

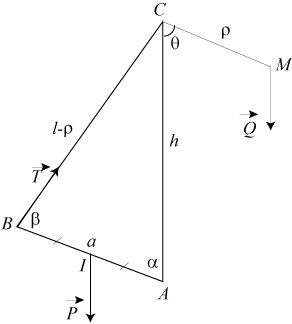
a = longueur du pont-levis = AB l = longueur du treuil = BC+CM P = poids du pont-levis Q = poids du contre-poids

Calcul de la tension du treuil : le pont étant en équilibre, la somme des moments des forces s'y exerçant est nulle :  ; on obtient .

 
 

On trouve un pontlevis à système Bélidor à Fort l'Ecluse (non loin de Genève).

Autres courbes définies mécaniquement : la courbe du seau d'eau, la courbe du danseur de corde.
 

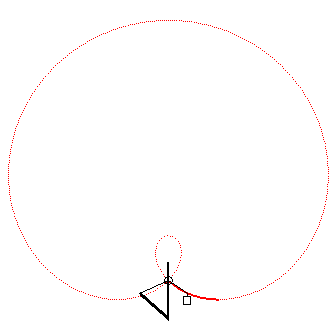
Cas où la courbe du pont-levis est une portion de limaçon de Pascal

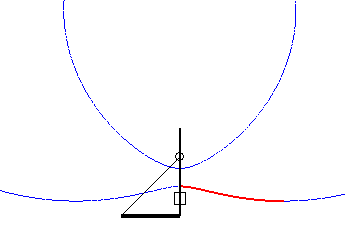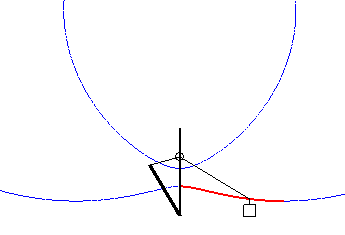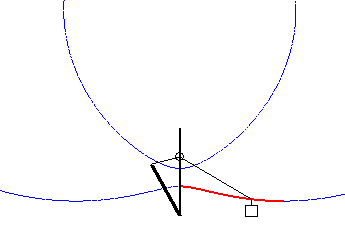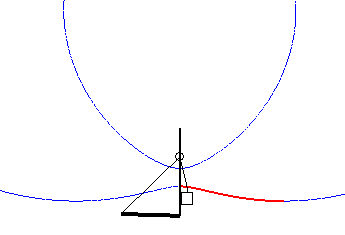
Cas où la courbe du pont-levis est une portion d'ovale de Descartes.

 

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL  2022