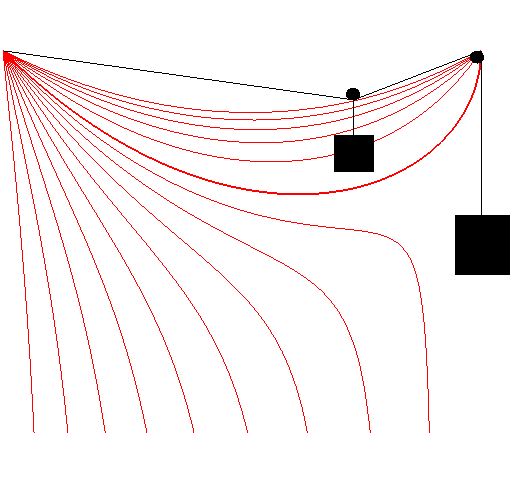
La courbe du danseur de corde est le lieu des pieds d'un funambule marchant sur une corde attachée à un point fixe à l'une de ses extrémités, passant par une poulie située à même hauteur que l'extrémité attachée, et tendue par un contre-poids attaché à l'autre extrémité.
Si k est le rapport masse du contre-poids sur masse de l'homme, l'extrémité attachée en O et la poulie en A(a, 0), l'axe Oy vers le bas, les lois de la statique donnent :
 

Équation cartésienne : , avec . Paramétrisation cartésienne : . Portion de quartique rationnelle d'équation . Cas particuliers : a = b : strophoïde droite ; a = 0 : kappa.

 

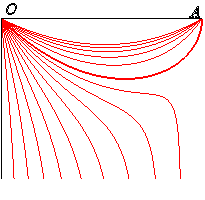Si k < 1 (le poids du funambule dépasse celui du contre-poids), la courbe possède une asymptote verticale x = b = ka : il est donc remarquable de constater que le funambule ne tombe pas tant qu'il n'a pas dépassé une abscisse limite. Sinon, c'est un arc joignant O à A.

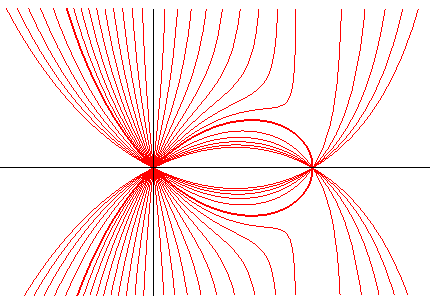Vue des courbes complètes ; en gras, le cas k = 1, qui est une strophoïde droite.  Quand k tend vers l'infini, la courbe se rapproche d'un kappa.

 

Sans poulie, la courbe décrite par les pieds du funambule est une ellipse.

Comparer avec la courbe du seau d'eau.
 

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL  2010