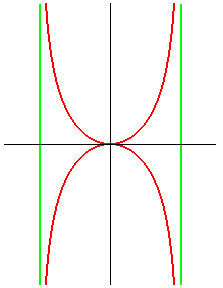Équation polaire :  (ou  si l'on veut que la courbe soit présentée comme la lettre x) Équation cartésienne :  ce qui peut s'écrire . Paramétrisation cartésienne : . Quartique rationnelle. Aire de la portion comprise entre la courbe et ses deux asymptotes : pa2.

Le kappa est le lieu du sommet M d'une équerre zMB dont le côté (zM) passe par O, tandis que le sommet B glisse sur la droite Oy .

En ce sens, le kappa est une glissette de bases O et Oy et de glissantes Oz et B (voir sur la page glissette, cas particulier n°5).

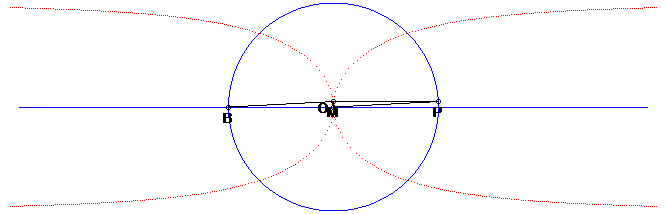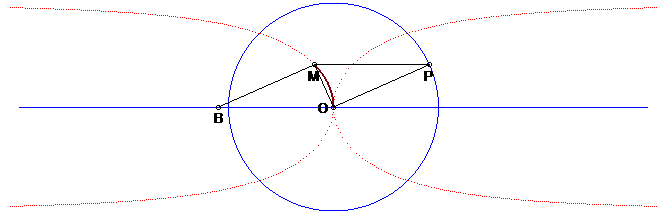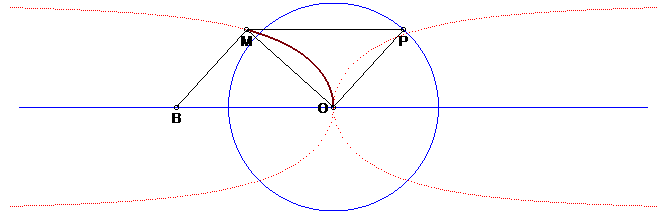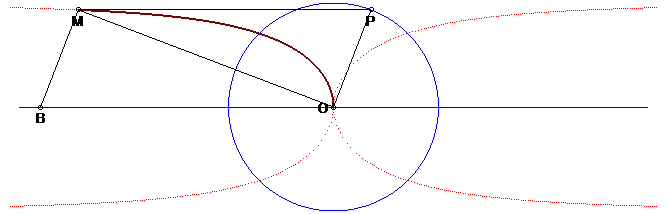
Autre construction, équivalente à la précédente : le kappa est le lieu du sommet M d'un triangle rectangle en O : POM, P décrivant un cercle de centre O et (PM) restant parallèle à une droite fixe. Cette construction est un cas limite de la construction d'une courbe comme lieu de l'orthocentre d'un triangle de base fixe (ici, réduite au point O) et de sommet décrivant une courbe (ici P), voir par exemple la construction du bicorne.

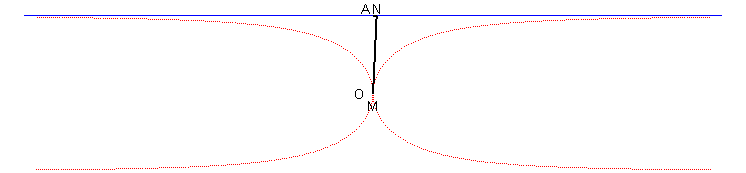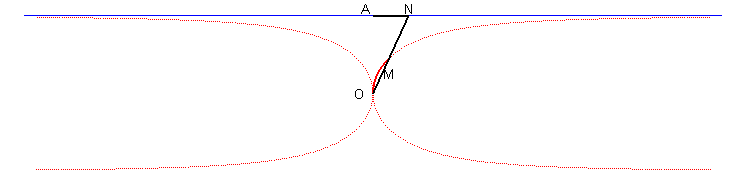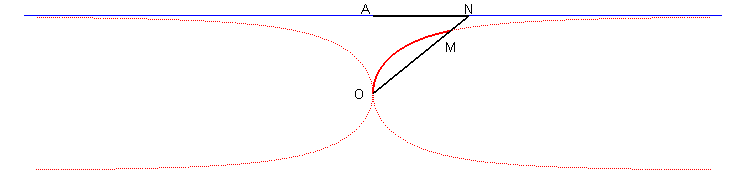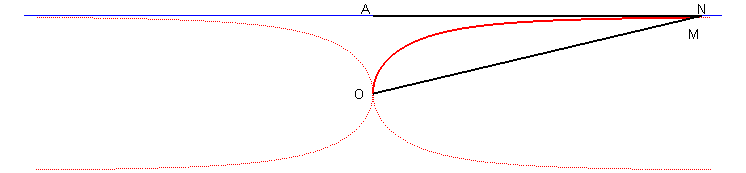
Troisième construction : une droite variable (D) passant par O coupe la droite x = a en N ; le kappa est le lieu des points M de (D) tels que OM = AN où A(a,0).

Le kappa est la radiale de la tractrice ainsi qu'un cas particulier de nœud.

Voir la construction de la strophoïde droite à partir du kappa.

Ne pas confondre avec la puntiforme.

On peut s'intéresser plus généralement au mouvement plan sur plan dit du kappa, le plan mobile étant le plan lié à l'équerre ci-dessus (le kappa étant alors la roulette du sommet de cette équerre).

En reprenant les notations de cette page, on a  : .
La base est donc la campyle d'Eudoxe d'équation polaire , la roulante la parabole , et les roulettes les courbes :  : dans le mouvement du kappa, il y a échange de la base et de la roulante par rapport au mouvement conchoïdal.
 

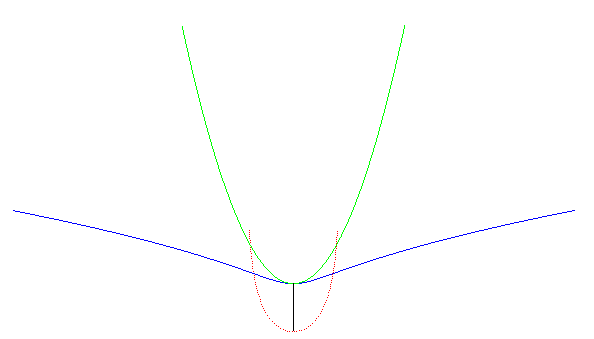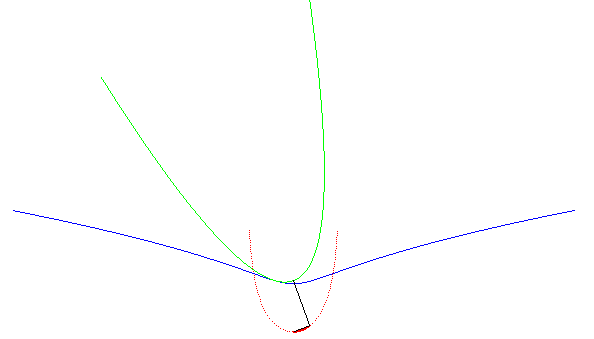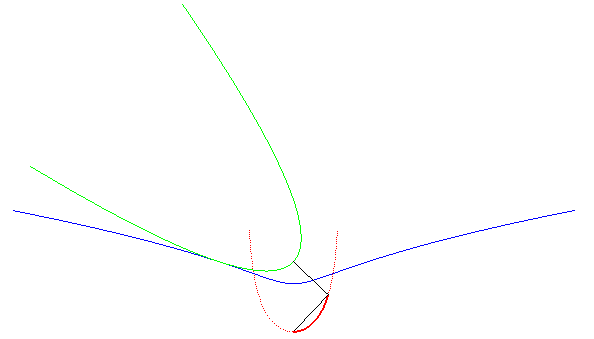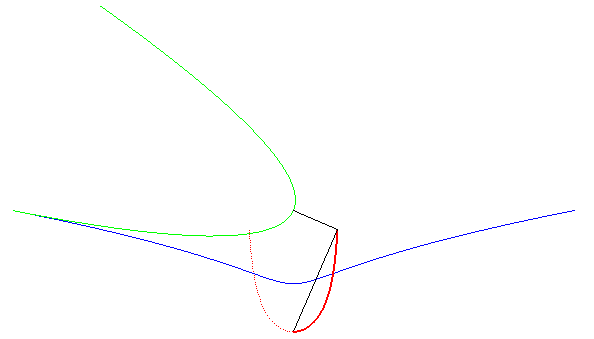Le kappa est une roulette du mouvement associé au roulement d'une parabole sur une campyle.

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL 2019