PUNTIFORME
Bullet
nose curve, Kohlenspitzenkurve
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
PUNTIFORME
Bullet
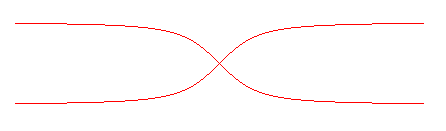
nose curve, Kohlenspitzenkurve

| Courbe étudiée par Pieter
Schoute en 1883.
Du latin punctum "point", mais puntiforme signifie : en forme de pointe. En anglais, bullet nose signifie "extrémité de balle" et en allemand, kohlenspitzenkurve "pointe de crayon" (nom donné par Schoute). |
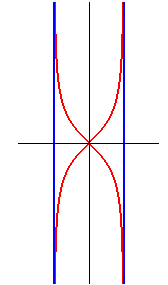 |
Équation cartésienne : Paramétrisation cartésienne : Quartique rationnelle. Aire entre la courbe et les asymptotes : 4ab. |
La puntiforme est l'image de l'hyperbole ( ici )
par une inversion biaxiale (d'axes ceux de l'hyperbole), définie
ici par :
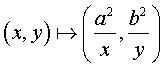
Ne pas confondre avec le kappa.
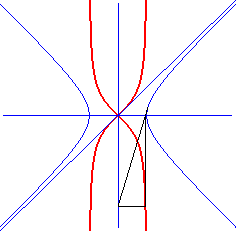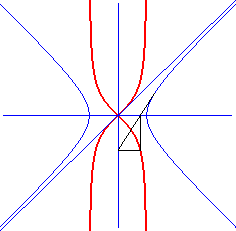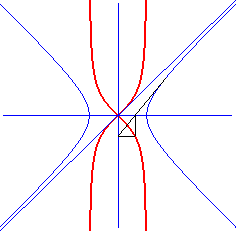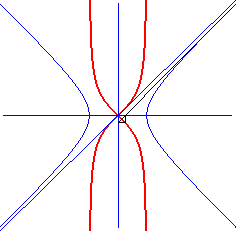
| Ci-contre, famille des quartiques d'équation La puntiforme est obtenue pour k = 1 (limite entre les courbes bleues et rouges). |
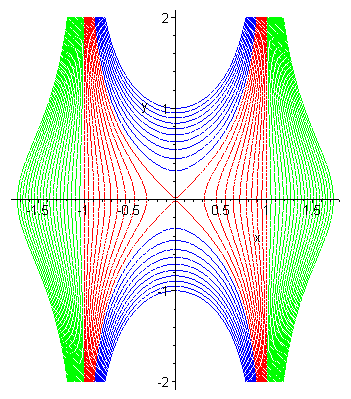 |
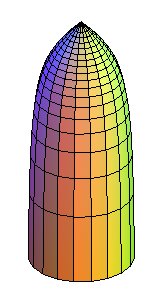
| La rotation d'une demi puntiforme autour d'un de ses
axes (équation |
 |

| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2021