Courbe de Kiepert

COURBE DE KIEPERT
Kiepert curve, Kiepertsche Kurve

Courbe étudiée par W. Roberts et par L. Kiepert en 1870.
Friedrich Wilhelm August Ludwig Kiepert (1846-1934) : mathématicien allemand.
Autre nom de cette courbe : lemniscate à 3 pôles.

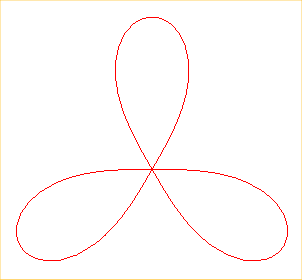
Équation tripolaire :

où (ABC) est le triangle équilatéral A(d), B(dj), C(dj²).
Équation polaire :

avec

.
Équation cartésienne :

.
Équation complexe :

.
Sextique tricirculaire de genre 1.

La courbe de Kiepert est la spirale sinusoïdale d'ordre 3, c'est donc un cas particulier de cassinienne , et de courbe de Goursat ; elle est au triangle équilatéral ce que la lemniscate de Bernoulli est au bipoint.

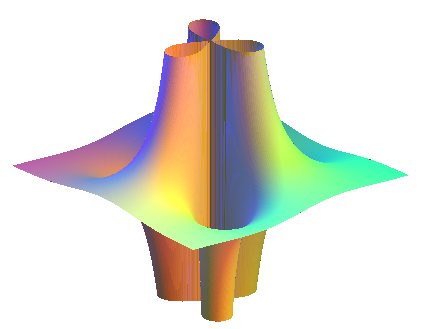
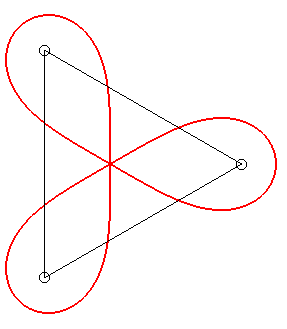
Les sections horizontales des deux surfaces associées à la fonction complexe , d'équations sont des courbes de Kiepert.

Son inverse de centre O est la cubique de Humbert.

Comparer avec le trifolium régulier.

courbe suivante courbe précédente courbes 2D courbes 3D surfaces fractals polyèdres