Les courbes de Goursat d'ordre n sont les courbes ayant les symétries d'un polygone régulier à n côtés, c'est-à dire dont le groupe des isométries la laissant invariante est celui de ce polygone, à savoir le groupe diédral d'ordre 2n.

Une courbe est donc une courbe de Goursat d'ordre n ssi elle est invariante par une rotation d'un n-ième de tour (et non invariante par une rotation d'angle plus petit) et qu'elle possède un axe de symétrie, ou ssi elle possède n axes de symétrie exactement.
 
 

Équation polaire générale d'une courbe de Goursat d'ordre multiple de n :	Équation cartésienne :
avec f paire (ou impaire) et de plus petite période par rapport à  : ,	avec f paire par rapport à y et
d'où la famille :  (transformée de Brocard de la courbe ).	forme correspondante : 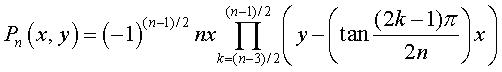avec  ; pour n pair, pour n impair

Exemples : les rosaces:  et leurs inverses les épis, les spirales sinusoïdales : .

Cas particuliers :

1) n multiple de 2 :

Équation polaire :  (ou )

Équation cartésienne : ,  autrement dit :  (axes Ox et Oy), ou encore  (axes ).

Exemples avec deux axes de symétrie exactement :
degré 2 : les ellipses , les hyperboles .
degré 4 : la lemniscate de Bernoulli , celle de Gérono ,  la puntiforme, la campyle d'Eudoxe, le kappa, le double U, la quartique de Kulp, la trisectrice de Delanges, les courbes d'Alain, les courbes du diable.
ETC....
 

2) n multiple de 3 :

Équation polaire :

Équation cartésienne :  Rem :

Exemples avec trois axes de symétrie exactement :
degré 3 : le trèfle équilatère : et la cubique de Humbert : (qui sont à similitude près les seules cubiques 3-courbes de Goursat) .

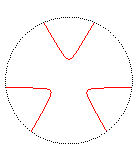
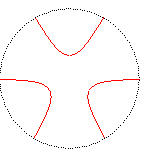degré 4 : les hypotrochoïdes de paramètre q = 3: (dont la deltoïde, k = 1 et le trifolium régulier, k = 2) 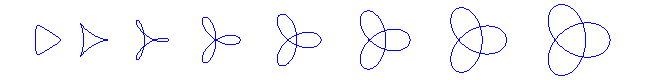, les conchoïdes de trifolium régulier, la courbe de Kiepert, la quartique de Klein, la quartique de Loriga,

3) n multiple de 4 :

Équation polaire :   ou , ou encore  avec f paire par rapport à la deuxième variable.

Équation cartésienne : , autrement dit  , ou encore  avec f symétrique.

Exemples avec quatre axes de symétrie exactement :
degré 4 : la cruciforme équilatère : , les quartiques de Salmon .

degré 6 :  les hypotrochoïdes de paramètre q = 4 : (dont l'astroïde et le quadrifolium), les conchoïdes de rosaces de paramètre 4  avec b non nul , le moulin à vent,
la sextique de Loriga :.

4) n multiple de 5 :

Équation polaire générale :

Équation cartésienne générale : .

Exemples avec cinq axes de symétrie exactement :
degré 5 : équation cartésienne générale : (l'un des 3 nombres k, k', k" pouvant être choisi arbitrairement).
(k,k',k")=(1,0,0) donne l'épi d'ordre 5 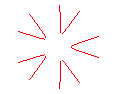,  donne la courbe à 5 points doubles : 
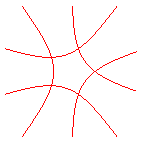
(k,k',k")=(0,–1,0.2) donne 
 

5) n multiple de 6 :

Équation polaire générale :

Équation cartésienne générale : .

Exemples avec six axes de symétrie exactement :
degré 6 :  et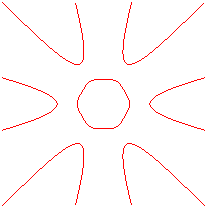 
 

Exemples de familles infinies :

    - les conchoïdes de rosace :  sont de Goursat d'ordre n (sauf pour n pair et b nul : ordre 2n)

    - toutes les familles de courbes définies symétriquement à partir de n points , sommets d'un polygone régulier (cf. le principe de Curie) ; en particulier  les courbes  ( : courbes isophoniques,  : équipotentielles de Cayley,  : ?,  : cercles), les courbes de Loriga : , et les cassiniennes : .
 
 

Toutes les courbes d'équation polaire  avec f  - périodique (m et n premiers entre eux) et paire (ou impaire) sont de Goursat d'ordre multiple de n. Exemple ci-contre :  avec n = 5, m = 3.
Plus généralement, f étant une fonction complexe, ayant les mêmes propriétés, la courbe de paramétrisation complexe  est de Goursat d'ordre multiple de n (le cas précédent étant le cas où f est réelle). Dans ce cas rentrent les épi- et hypotrochoïdes (). Le cas plus général 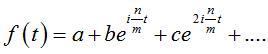 donne des polytrochoïdes. Ci-contre, la tritrochoïde obtenue pour .
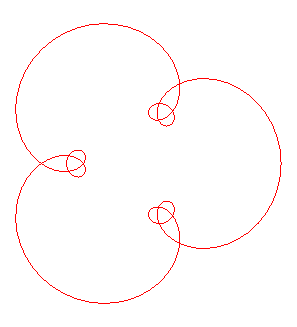f ayant les mêmes propriétés, la courbe de paramétrisation complexe est, elle aussi, de Goursat d'ordre multiple de n. Dans ce cadre rentrent les courbes à rayon sinusoïdal généralisées.
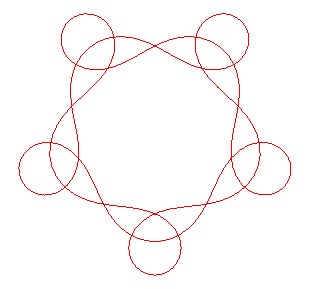
Les courbes définies par une équation intrinsèque :  avec f  paire, L-périodique et telle que   soit un rationnel m/n non entier (m premier avec n) sont de Goursat d'ordre multiple de n. De plus, l'entier m est l'indice de rotation de la courbe. Forme équivalente :  avec f  paire,- périodique de moyenne nulle. Exemple ci-contre : n = 5, m = 3 , . On obtient ainsi toutes les courbes de Goursat d'ordre n d'indice de rotation non nul.

Classification des courbes génériques sphériques , de Goursat d'ordre n, ayant exactement n points doubles.

Il y en exactement de 3 types, dont l'un n'a des représentants que pour n impair :
 

	2 points doubles	3 points doubles	4 points doubles	5 points doubles
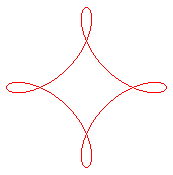
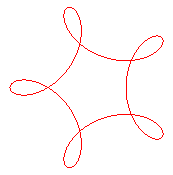
Premier type Hypotrochoïde de paramètre q = n, sauf pour n = 2. Indice de rotation : n -1	Lissajous x = cos t , y = sin 3t.
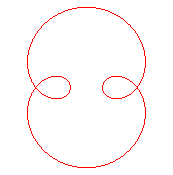
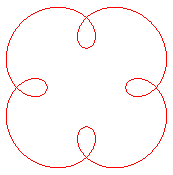
Deuxième type Épitrochoïde de paramètre q = n. Indice de rotation :  n +1
Troisième type Conchoïde de rosace de paramètre n/2 Indice de rotation : 2

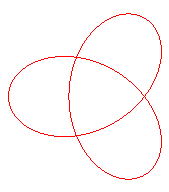Voir aussi les surfaces de Goursat, et les surfaces à symétries de rotation.
 
 

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL  2011