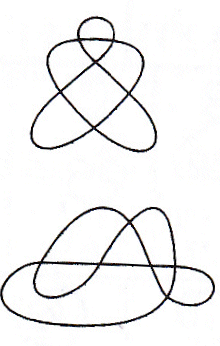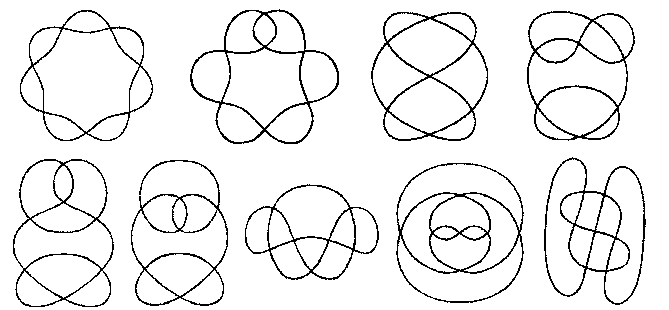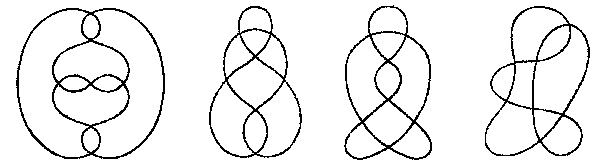Notion étudiée par Whitney en 1937 et par Arnold en 1994. Sources :  Marcel Berger, La taxonomie des courbes,  Pour la Science N°297, Juillet 2002 Article de Guy Valette.

Une courbe (fermée) générique, plane (ou sphérique), est (au sens d'Arnold) une classe d'équivalence de courbes fermées du plan ou de la sphère dont tous les points multiples sont doubles à tangentes distinctes, deux courbes étant identifiées si elles sont image l'une de l'autre par un difféomorphisme du plan (ou de la sphère). Cette notion est une généralisation de celle de courbe de Jordan au cas où les courbes ont des points de croisement.
Par courbe fermée on entend ici l'image C de [0,1] par une application f de [0,1] dans le plan (ou la sphère), de classe C¹, de dérivée jamais nulle, telle que f (0) = f (1) et f ' (0) = f ' (1). La condition des points multiples à tangentes distinctes s'écrit : pour tout point M de C il existe soit une, soit deux valeurs t₁ et t₂ de [0,1[ telles que f(t₁) = f(t₂) et dans ce dernier cas, 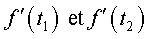 sont non colinéaires.
La distinction entre courbe plane ou sphérique est importante ; par exemple, un huit 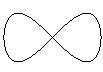 est équivalent à un limaçon à boucle  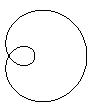sur la sphère mais pas dans le plan.
Voici divers invariants permettant de classer les courbes génériques :

1) le nombre (forcément fini) n de points doubles ; ils déterminent n + 2 régions dans le plan, et la courbe est réunion de 2n arcs joignant deux points doubles consécutifs. 2)  l'indice de rotation (voir les notations) :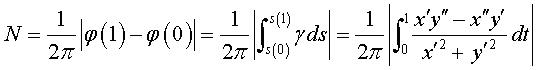, mesurant le nombre de fois que la tangente fait un tour complet sur elle-même. On démontre que 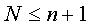 et que n et N ont parité contraire. Ces propriétés sont conséquence du résultat suivant (formule de Whithney) : un parcours étant choisi sur la courbe, un point double est décrété positif si lors du deuxième passage à ce point double, le premier passage s'était fait de gauche à droite, et négatif sinon ; si n+ est le nombre de points doubles positifs et n- le nombre de points doubles négatifs, alors N = |n+ - n-| ± 1. 3) le diagramme de Gauss (voir l'article ci-dessus).

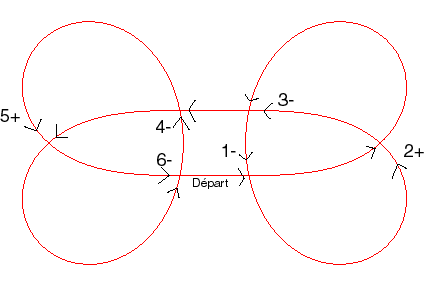
Ici il y a n = 6 points doubles, 8 régions, 12 arcs. Indice de rotation N = 3 = |2 - 4|+1

Une courbe générique est dite irréductible si lui enlever un point double la laisse toujours connexe (par exemple, un huit n'est pas irréductible).

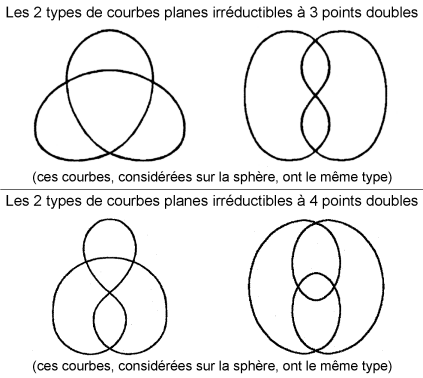
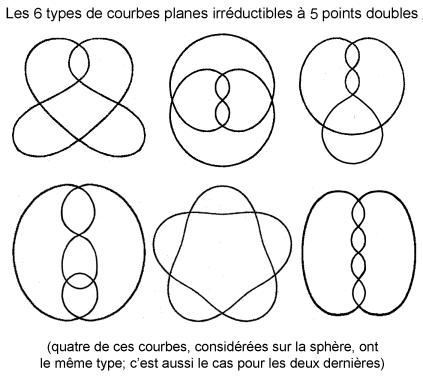
Ci-dessous, classification des courbes génériques planes et sphériques irréductibles ayant jusqu'à 7 points doubles :
  0 point double :  , aucune avec 1 ou 2 point double ,
 

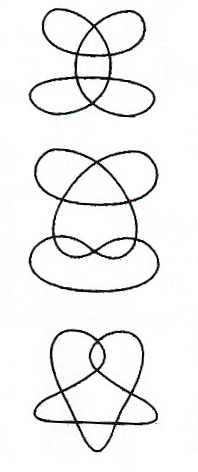
n = 6 (Arnold 1994) : 5 courbes sphériques fournissant 22 courbes irréductibles planes	n = 7 (Guy Valette 2004) : 13 courbes sphériques fournissant 78 courbes irréductibles planes

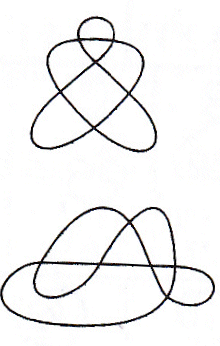
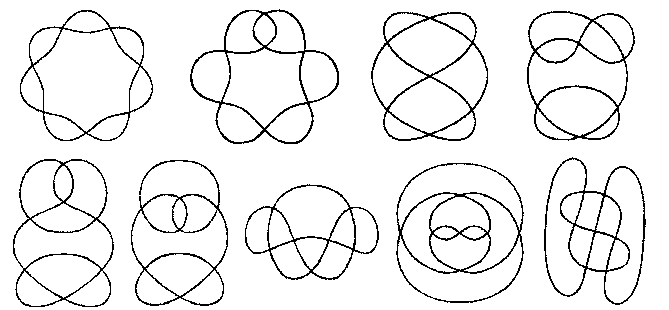
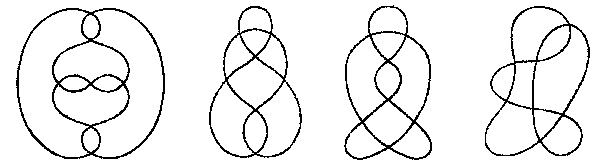
Comparer avec les noeuds premiers.
Voir à courbe de Goursat la classification des courbes génériques à n points doubles ayant les symétries d'un n-gone régulier.
 

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL  2013