Courbe

COURBE
Curve, Kurve

C'est une très bonne question et je ne vous remercie pas de me l'avoir posée !

En effet, définir de façon générale une courbe plane est impossible :

Si l'on dit qu'une courbe est une partie du plan homéomorphe à une droite, alors n'est pas une courbe.

Si l'on dit qu'une courbe est une partie du plan dont tout point possède un voisinage homéomorphe à la droite ou à la demi-droite, autrement dit, une variété topologique de dimension 1, alors n'est pas une courbe.

Si l'on désigne par courbe topologique cette dernière notion, alors toute composante connexe d'une courbe topologique est une courbe topologique, et il n'y a, à homéomorphisme près, que 3 courbes topologiques connexes : le cercle S¹, la droite R et la demi-droite R₊ ; dans le premier cas la courbe topologique est dite "fermée", ou "courbe de Jordan" dans le deuxième cas "ouverte", et le troisème "semi-ouverte".

Si l'on dit qu'une courbe est une partie du plan dont tout point possède un voisinage réunion d'un nombre fini de parties homéomorphes à la droite, alors n'est pas une courbe.
Si l'on dit qu'une courbe est une partie du plan dont tout point possède un voisinage réunion d'une famille dénombrable de parties homéomorphes à la droite, alors est une courbe (c'est une rosace qui est dense dans le disque avec n irrationnel).

Si l'on dit qu'une courbe est une partie du plan image d'un intervalle de R par une fonction continue, (autrement dit, le support d'un arc paramétré continu), alors l'hyperbole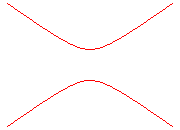, n'est pas une courbe, maisest une courbe, et plus généralement toutes les parties compactes connexes et localement connexes, qui sont exactement les images continues de [0,1], sont des courbes.

Si l'on dit qu'une courbe est une partie de R² d'équation f(x, y)= 0 avec f continue, voire même infiniment dérivable, alors une bande de largeur non nulle est une courbe.

Si l'on dit qu'une courbe est une partie de R² d'équation f(x, y)= 0 avec f dérivable de différentielle jamais nulle, alors on n'obtient que des courbes simples (i.e.sans point double)...

Voir à courbe générique une notion plus générale que celle de courbe topologique fermée simple.

courbe suivante courbe précédente courbes 2D courbes 3D surfaces fractals polyèdres