COURBE DE GAUSS
Gaussian
curve, Gauss-Kurve
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
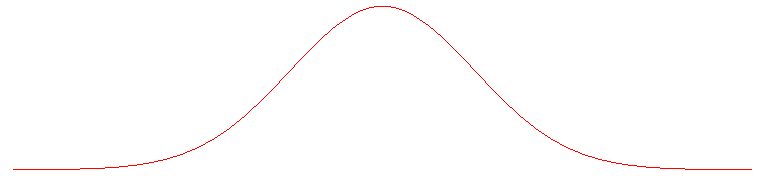
COURBE DE GAUSS
Gaussian
curve, Gauss-Kurve

| Courbe étudiée par de Moivre en 1718 et
par Gauss en 1809.
Carl Friedrich Gauss (1777 -1855) : astronome, mathématicien et physicien allemand. Autre nom : courbe en cloche (de Gauss), gaussienne. |
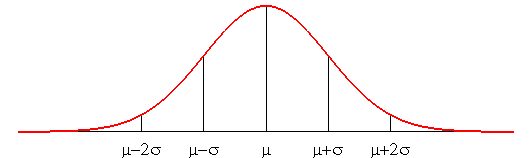
L'aire entre la courbe et l'asymptote est égale à N ; l'aire de la portion entre m - s et m + s vaut approximativement 2/3 de N ; entre m - 2s et m + 2s elle vaut approximativement 96% de N . |
Équation cartésienne : Par exemple, le nombre |
La courbe de Gauss est la courbe de la fonction de densité d'une loi de probabilité normale.
Pour,
on obtient la courbe de Gauss dite "centrée réduite".
Ne pas confondre la courbe en cloche de la loi de Gauss avec celle de la loi de Cauchy, qui n'est autre qu'une cubique d'Agnesi.
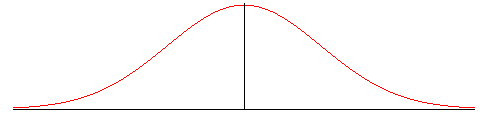
Si l'on se dégage de l'aspect probabiliste, la
courbe de Gauss a les caractéristiques suivantes :
| Equation cartésienne : Aire entre la courbe et l'asymptote : |
 |
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2019