CUBIQUE D'AGNESI
Witch
of Agnesi, Versiera

| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
CUBIQUE D'AGNESI
Witch
of Agnesi, Versiera

| Courbe étudiée par Pierre de Fermat en
1630 puis par Guido
Grandi en 1703 et par Maria Gaetana Agnesi en 1748.
Autres noms : versiera (= diablesse en italien), cloche de Cauchy. Explication de ces diableries : Grandi donne à cette courbe en 1703 le nom latin de versoria (signifiant "corde servant à virer de bord", du verbe versare, "tourner"). En 1748, Agnesi change le nom en versiera qui est aussi une aphérèse de avversiera, signifiant "sorcière" en vieil italien (du latin adversarius : adversaire, nom métaphorique du Diable). Enfin, John Colson, dans sa traduction de l'oeuvre d'Agnesi, utlise l'expression witch (sorcière) of Agnesi, que les anglophones ont conservée. Maria Gaetana Agnesi : mathématicienne italienne (1718-1799) :  |
 |
| Équation cartésienne : Cubique rationnelle à point isolé (situé à l'infini dans la direction de Oy). Paramétrisation cartésienne : Aire du domaine délimité par la courbe et son asymptote : Volume du solide engendré par la révolution de la courbe autour de son asymptote : |
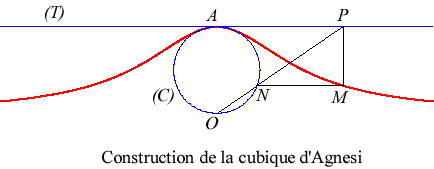
| La cubique d'Agnesi est l'hyperbolisme
du cercle par rapport à l'un de ses points et la tangente diamétralement
opposée à ce point.
Ici, le cercle est le cercle de diamètre [OA], avec A(0, a). C'est donc un cas particulier d'oeuf de Granville. |
 |
| Comme l'anguinée, c'est une projection de l'horoptère. |
 |
| L'équation cartésienne montre que la cubique
d'Agnesi est un cas particulier d'hyperbole
cubique.
La transformation homographique : |
La perspective d'une cubique d'Agnesi est une parabole divergente. La cubique d'Agnesi (en rouge en haut) est projectivement
|
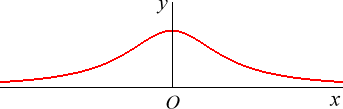
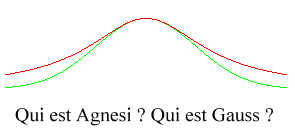
| Il ne faut pas confondre la cubique d'Agnesi avec la
courbe
en cloche (de Gauss), courante en probabilités, qui est transcendante
!
Mais la cubique d'Agnesi est aussi utilisée en probabilités, car c'est la courbe de la fonction de densité d'une loi de Cauchy (d'où le nom de "cloche de Cauchy"). |
 |
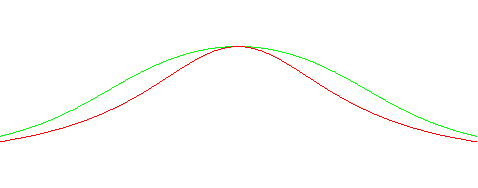
| Par contre, une autre cubique (en vert ci-contre) ressemble
aussi à la cubique d'Agnesi :
Equation cartésienne : Equation polaire : Cette courbe est aussi un cas particulier d'hyperbole cubique, mais elle n'est pas rationnelle. Voir la rotation 3D de cette courbe à "surface de révolution". |
 |
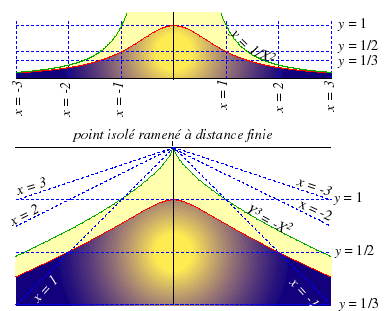
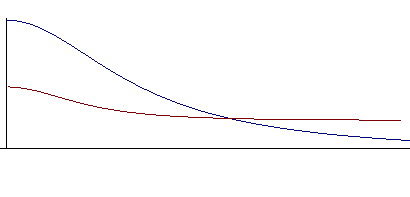
| Particularité du domaine homogène limité
par la courbe Mais si l'on accepte que cette intégrale soit nulle (fonction impaire), ce centre a pour coordonnées De même, la partie de ce domaine située à droite de l'axe Oy n'a pas de centre de gravité à distance finie, car |
 |
La cubique d'Agnesi est aussi une directrice du conoïde de Plücker et du parapluie de Cartan.
Comparer cette courbe avec la visiera et la quartique de Külp.
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2019