ANGUINÉE
Anguinea
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
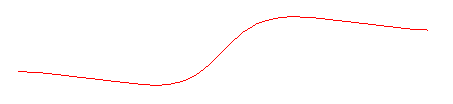
ANGUINÉE
Anguinea

| Courbe étudiée par L'Hospital et Huygens
en 1692 puis par Newton en 1701.
Du latin anguis "serpent, hydre, dragon" (au choix !), nom donné par Newton. Autres noms : anguinea, cubique serpentine. |
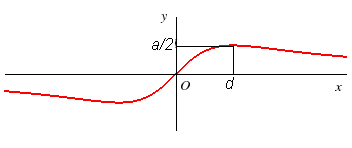 |
Équation cartésienne : Paramétrisation cartésienne : Équation polaire : |
|
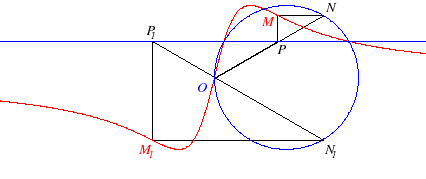
L'anguinée est l'hyperbolisme du cercle par rapport à un point O de ce cercle et une droite parallèle au diamètre passant par O. Ici, le cercle est le cercle de diamètre [OA] avec A(a, 0) et la droite, y = d. |
 |
|
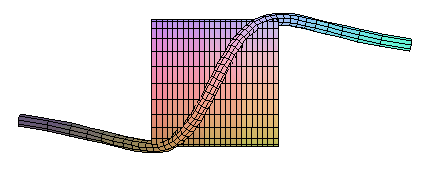
Comme la cubique d'Agnesi, c'est une projection de l'horoptère. |
 |
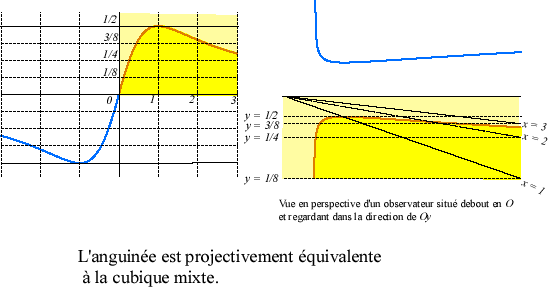
Pour ramener le point isolé à l'infini à
distance finie, on peut utiliser la transformation homographique :
qui transforme l'anguinée
en la cubique mixte
:
ayant son point isolé en O.
Dans la figure ci dessous, nous avons utilisé
au lieu de
pour
plus de lisibilité.
L'anguinée est une directrice du conoïde de Plücker.
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2016