Anamorphose

ANAMORPHOSE
Anamorphosis

Procédé étudié par Jean-François Nicéron en 1636.
Du grec ana "en remontant", qui marque le "retour vers", et morphe "forme".

Le terme anamorphose désigne d’une façon générale, la transformation qui à un objet fait correspondre l'objet dont il est l'image virtuelle dans un système optique, pour un observateur donné situé à distance finie ou infinie.

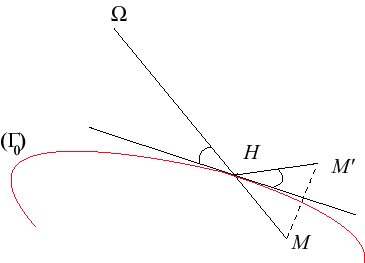
Dans le plan, nous définirons l'anamorphose associée à une courbe (G₀) (le miroir) et un point W (l'observateur) comme la relation qui à tout point M fait correspondre son (ou ses) symétrique(s) par rapport au miroir en partant de W, c'est-à-dire tout point M' symétrique de M par rapport à la tangente en H à (G₀), H étant un point d'intersection de la droite (WM) avec le miroir (G₀) ; de la sorte, un rayon lumineux issu de M' arrive dans les yeux de l'observateur après réflexion en H et M est une image virtuelle de M'. En clair, l'observateur croit voir M, alors qu'il voit M'.

On obtient les coordonnées de M' par la relation où est le vecteur normal à (G₀) en H ;
par exemple, si (G₀) est le cercle trigonométrique et l'observateur à l'infini dans la direction de Oy, et M(x, y), M'(x', y'), on a avec et u = x (donc ), on obtient (voir figure ci-dessous).
Pour une courbe (G₀) paramétrée en complexes par u(t), et un observateur situé à l'infini dans la direction de Oy, la relation entre M(z) et M'(z') s'obtient en éliminant t entre les relations .

Cette relation transforme une courbe (G) en une courbe (G'), dite anamorphose de la première.

Exemples :

- une anamorphose rectiligne ((G₀) = droite) n'est autre qu'une réflexion.

- anamorphose circulaire :

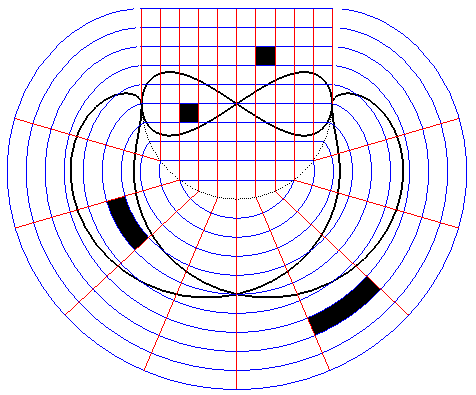Vue d'une anamorphose circulaire pour un observateur situé à l'infini dans la direction de Oy, avec transformation d'un quadrillage et d'une courbe.
Le quadrillage courbe est le quadrillage réel dont l'image virtuelle est le quadrillage de départ.

L'anamorphose circulaire dans le plan est identique à la restriction au plan de l'anamorphose cylindrique en 3D, comme le montre cette photo.

Voici inversement l'image virtuelle d'un quadrillage réel (ceci nécessite d'inverser la relation M -> M')

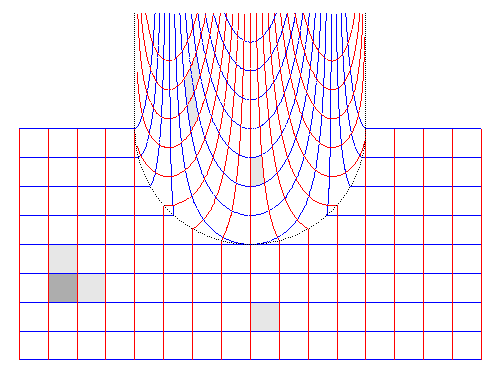Anamorphose cylindrique obtenue à l'aide du logiciel povray (Alain Esculier)

Pour certains auteurs, le terme d'anamorphose désigne plus simplement la transformation qui à un objet fait correspondre son symétrique par rapport à un miroir courbe.

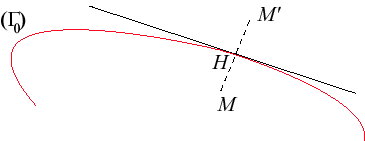Dans le plan, l'anamorphose (au sens n°2) associée à une courbe (G₀) (le miroir) est la relation qui à tout point M fait correspondre son (ou ses) symétrique(s) par rapport au miroir, c'est-à-dire tout point M' symétrique de M par rapport à un projeté orthogonal H de M sur (G₀).

Contrairement à l'anamorphose vue précédemment, cette relation est symétrique.

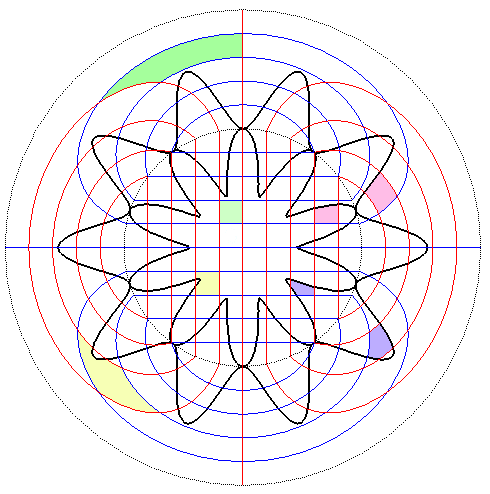Vue d'une anamorphose circulaire (au sens n°2) avec transformation d'un quadrillage et d'une courbe.
Pour un miroir circulaire de rayon a centré en O, les formules de transformations en coordonnées polaires sont .
Les courbes bleues et rouges sont des quartiques.

Voir aussi l'anamorphose en 3D.

Site en anglais : www.anamorphosis.com/

Site en français : members.aol.com/ManuelLuque3/miroirs.htm#anamorphoses

courbe suivante courbe précédente courbes 2D courbes 3D surfaces fractals polyèdres