Mixed cubic, gemischte Kubik

| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
|
Mixed cubic, gemischte Kubik |
 |
| Courbe étudiée par de Longchamps en 1890, qui lui a donné son nom. |
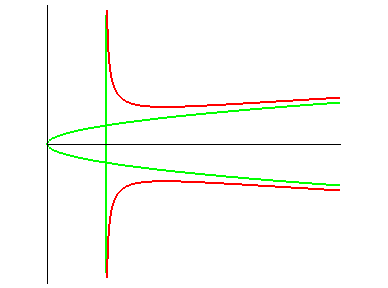 |
Équation cartésienne : ou Paramétrisation cartésienne : Cubique rationnelle à point isolé (O). Équation polaire : 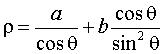
(s'écrivant |
Étant donné une parabole (P)
(ici d’équation
) et une droite (D) perpendiculaire à
l’axe de (P) (ici d’équation x = a),
la cubique mixte associée est le lieu du point M d’une droite
variable (D) passant par O recoupant (P)
en P et coupant (D) en Q tel que
; autrement dit la cubique mixte est la cissoïdale
de la parabole (P) et de la droite droite (D)
; c'est un cas particulier de cissoïdale
de Zahradnik.
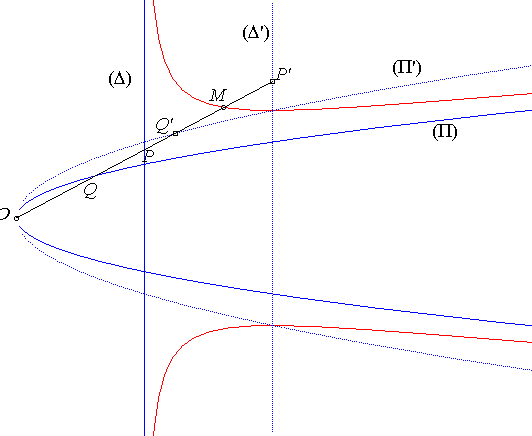
L’appellation cubique mixte vient de ce que cette courbe
possède une asymptote rectiligne ()
et une asymptote parabolique (
).
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL, Jacques MANDONNET 2001