
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
|
|
 |
| Curve studied by de Longchamps in 1890, who named it. |
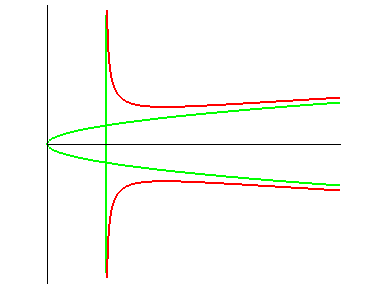 |
Cartesian equation: or Cartesian parametrization: Rational cubic with isolated point (O). Polar equation: 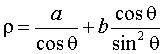
(written |
Given a parabola (P) (here
with equation
) and a line (D) perpendicular to the axis of
(P) (here, with equation x = a), the
associated mixed cubic is the locus of the point M on a variable
line (D) passing by O, cutting (P)
in P and cutting (D) in Q such
that
.
In other words, the mixed cubic is the cissoid
of the parabola (P) and the straight line (D);
it is a special case of Zahradnik
cissoid.
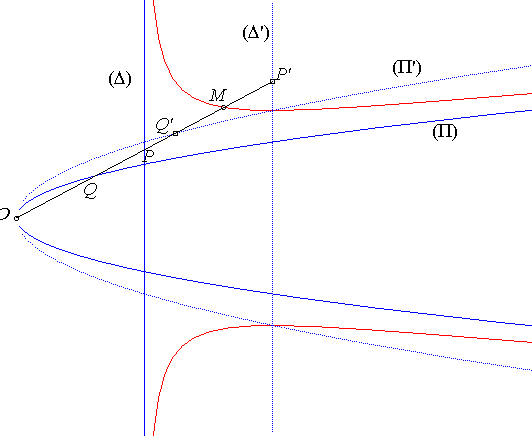
The name mixed cubic comes from the fact that this curve
has a linear asymptote ()
as well as a parabolic asymptote (
).
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2017