Courbe étudiée par A.-Abakanowicz en 1889. Bruno Abdank-Abakanowicz (1852-1900) : ingénieur polonais. Autre nom : intégrale de cercle.

 

Equation différentielle : . Paramétrisation cartésienne : . Courbe transcendante.

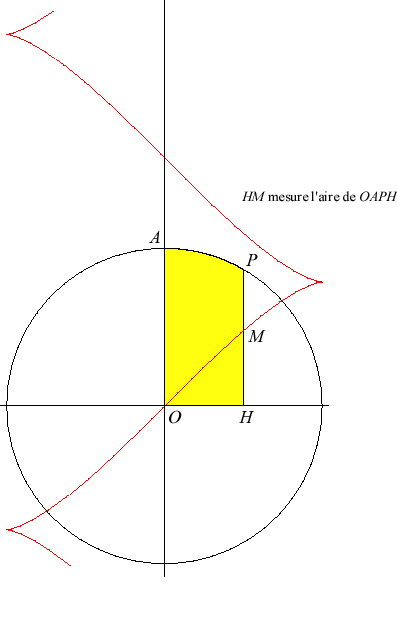
La quadratrice d'Abdank-Abakanowicz est la courbe tracée par l'intégraphe d'Abdank-Abakanowicz à partir d'un cercle. Cet appareil permettait, en partant d'une courbe de paramétrisation X = x(t), Y = y(t) donnée, de construire la courbe de paramétrisation cartésienne : X = x(t), Y =  . Pour la courbe qui nous occupe,  x(t) = R sin t et y(t) = R cos t.

Comme son nom l'indique, c'est une quadratrice (voir [Carrega] p 85).
 
 

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL , Jacques MANDONNET 2004