Une courbe est dite algébrique lorsqu’elle possède une équation cartésienne polynomiale à coefficients réels ; une courbe non algébrique est dite transcendante.

Le degré (ou parfois l'ordre) d'une courbe algébrique plane d'équation P(x, y) = 0 est le degré du polynôme P, supposé sans facteur carré ;
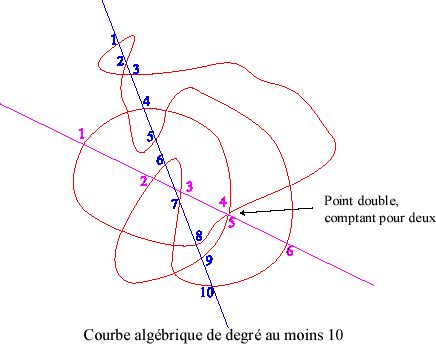
c'est aussi le nombre de points d'intersection, comptés avec les multiplicités, de la courbe avec une droite quelconque, dans le plan projectif complexe (et le nombre maximum de points d'intersection de la courbe avec une droite dans le plan affine réel est un minorant du degré et donne très souvent le degré).

Une courbe en spirale, ou ayant un point asymptote est donc forcément transcendante.

La notion de degré est projective, à savoir que toute homographie transforme une courbe algébrique en une courbe algébrique de même degré.
La courbe est dite décomposable si elle est réunion de courbes algébriques de degré plus petit et indécomposable dans le cas contraire, c'est-à-dire quand le polynôme P est irréductible dans .

Toute portion bornée d'une courbe algébrique peut être générée par un mécanisme articulé (théorème de Kempe).

Les courbes de degré 1 sont les droites, de degré 2 les coniques, de degré 3 les cubiques, de degré 4 les quartiques, de degré 5 les quintiques, de degré 6 les sextiques, de degré 7 les septiques, et de degré 8 les biquartiques.

Exemples de familles de courbes algébriques de degrés quelconques (pour des valeurs rationnelles des paramètres) : les courbes de Lissajous, les courbes de Lamé, les épi- et hypotrochoïdes, les rosaces, les conchoïdes de rosaces, les folioïdes, les nœuds, les épis, les larmes, les cassiniennes, les courbes de Clairaut, les spirales sinusoïdales.

Voir aussi à :
    - genre d’une courbe algébrique
    - courbe algébrique 3D
    - surface algébrique
 
 

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL , Jacques MANDONNET 2012