Courbe étudiée par Clairaut en 1726. Autre nom : (courbe) multiplicatrice de Clairaut.

 

Équation polaire :  avec n réel (ou ). Équation cartésienne : . Courbe algébrique si et seulement si n est rationnel.

Les courbes de Clairaut sont définies par leur équation polaire ci-dessus.

Exemples pour n positif (partie d'ordonnée positive) :

n = 1 : cercle	n  = 2 : oeuf double	n = 3 : folium simple
n = 1/2 : courbe du dipôle	n = 3/2	n = 5/2
n  = 1/3	n = 2/3	n = 4/3

Exemples pour n négatif (partie d'ordonnée positive) :

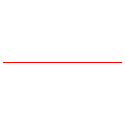
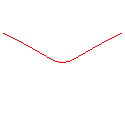
n = -1 : droite y = a	n  = -2 : kampyle d'Eudoxe	n = -3 : cubique duplicatrice
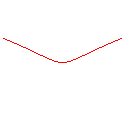
n =- 1/2 :  cf. quartique de Külp	n = -3/2	n = -5/2
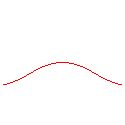
n  = -1/3 : cf cubique d'Agnesi	n = -2/3 : courbe de Roche.	n = -4/3

 
 

Les courbes de Clairaut sont les glissettes des spirales sinusoïdales ;  plus précisément, si on fait glisser la spirale sinusoïdale de paramètre n : sur une droite en un point fixe, la glissette du pôle est la courbe de Clairaut de paramètre 1/n  : . D'après le théorème d'équivalence glissette/roulette (voir à glissettes) les courbes de Clairaut sont donc aussi les roulettes rectilignes des développées des spirales sinusoïdales. Exemples :  pour  n = 1/2 : l'oeuf double est la glissette de la pointe de la cardioïde (cf. animation),  pour n = 2 :  la courbe du dipôle est la glissette du centre de la lemniscate de Bernoulli, pour n = -1/2 : la campyle d'Eudoxe est la glissette du foyer de la parabole, pour n = - 1/3 : la cubique duplicatrice est la glissette du foyer de la cubique de Tschirnhausen.

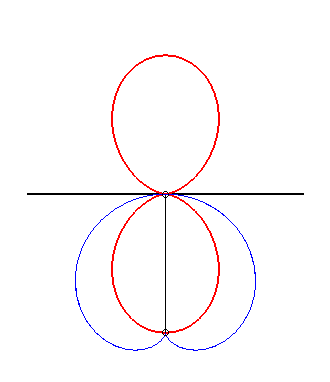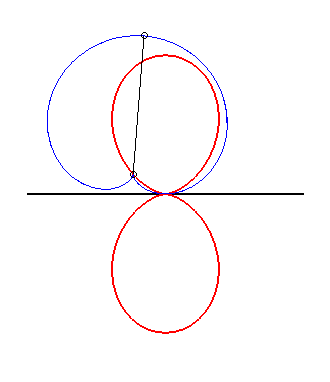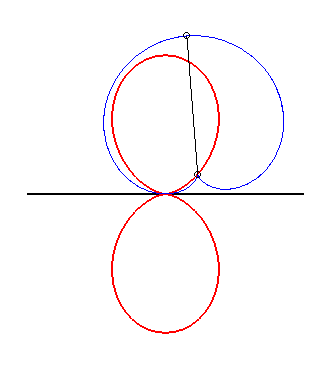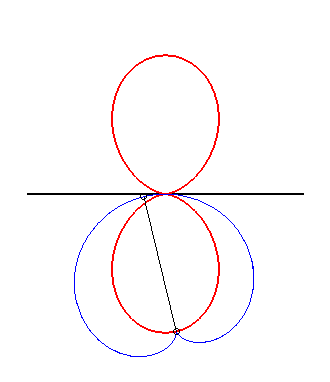Les trajectoires orthogonales des diverses courbes de Clairaut de paramètre n sont les courbes de Clairaut de paramètre 1/n. Ci-contre les cas n = 1 et 2.

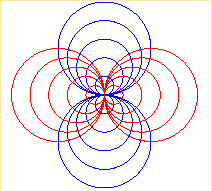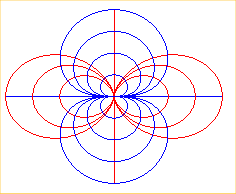La courbe de Clairaut de paramètre n est aussi la radiale de la courbe de Ribaucour de paramètre n + 1.
 
 

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL 2012