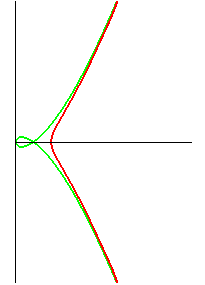
Vue avec la cubique asymptote 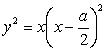 (en vert).

Équation polaire :  . Équation cartésienne : , soit  . Paramétrisation cartésienne :  . Cubique rationnelle (même polynomiale) à point isolé (le point (0,0), qui n'est pas atteint avec l'équation polaire).

Deux droites perpendiculaires D₁ (ici Ox) et D₂ (ici x = a) et un point O sur D₁ étant donnés, la cubique duplicatrice est le lieu d’un point M d’une droite variable D passant par O tel que le projeté de M sur D₁ ait pour projeté sur D un point de D₂.

Cette courbe est un cas particulier de parabole divergente et de courbe de Clairaut.

C'est aussi l'inverse du folium simple par rapport à son sommet "pointu",

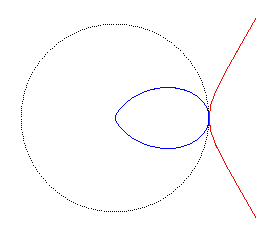
Comme son nom l'indique, c’est une duplicatrice : en effet, pour  , .
 
 

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL  2005