CLINOÏDE
Clinoid,
Klinoide
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
CLINOÏDE
Clinoid,
Klinoide
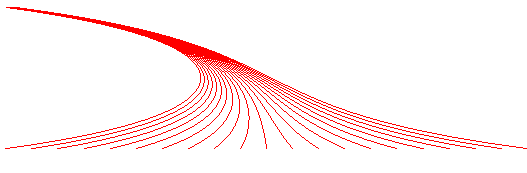
| Courbe étudiée et ainsi nommée par
Heinzerling
en 1869.
Du grec klinê : incliner ; au masculin, clinoïde est aussi un nom d'os crânien. |
Équation cartésienne :  ,
solution générale de l'équation différentielle  |
Pour b ou c nul, on obtient la courbe exponentielle.
Lorsque b = c = a/2, on obtient
la chaînette.
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2004