next curve previous curve 2D curves 3D curves surfaces fractals polyhedra

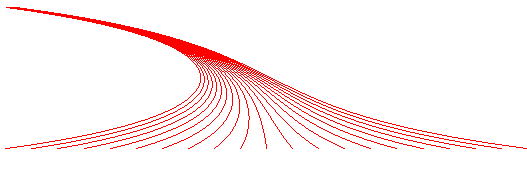
CLINOID

Curve studied and named by Heinzerling in 1869.
From the Greek klinê: to lean ; clinoid is also the name of a bone in the skull.

 
Cartesian equation: , general solution of the differential equation .

If b or c is equal to zero, we get the exponential curve.
When b = c = a/2, we get the catenary.
 
 
next curve previous curve 2D curves 3D curves surfaces fractals polyhedra

© Robert FERRÉOL  2017