Epi

Courbe étudiée par Cotes en 1722, Aubry en 1895.
Autre nom : spirale de Cotes (comprenant aussi la spirale de Poinsot).

Équation polaire :

(ou bien

) avec n réel > 0.
Courbe algébrique ssi n est rationnel, de degré n si n est entier impair, et de degré 2(n – 1) si n est entier pair.

Les épis sont les inverses de rosaces par rapport à leur centre.
Ce sont aussi les transformées de Brocard d'une droite, le pôle étant situé hors de la droite.

La courbe est formée d'une branche infinie obtenue pour :

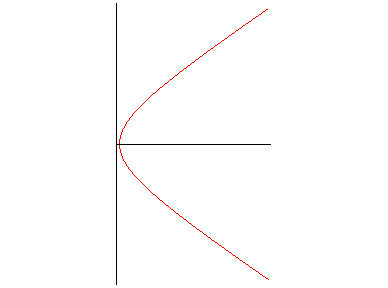
et de toutes ses images par des rotations d'angle

pour k entier.

Lorsque n est rationnel de numérateur p, et de dénominateur q, la courbe est symétrique par rapport à O ssi p ou q est pair.

Dans ce cas, la courbe est formée de 2p branches issues de la branche de base par rotations d'angles et + p.

Lorque p et q sont impairs, la courbe est formée de p branches issus de la branche de base par rotations d'angles .

Exemples :

n = 1 : droite
n = 2 : cruciforme
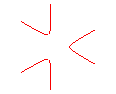
n = 3 : trèfle équilatère
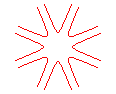
n = 4
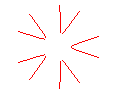
n = 5

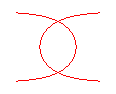
n = 1/2 :
trisectrice de Delanges
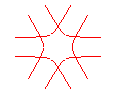
n = 3/2
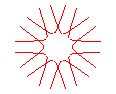
n = 5/2
n = 7/2
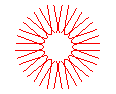
n = 9/2

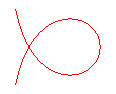
n = 1/3 : trisectrice de Maclaurin
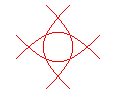
n = 2/3
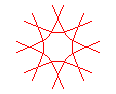
n = 4/3
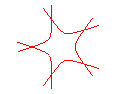
n = 5/3
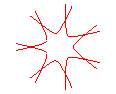
n = 7/3

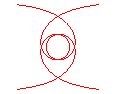
n = 1/4
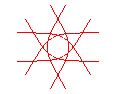
n = 3/4
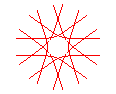
n = 5/4
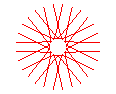
n = 7/4
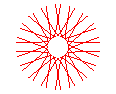
n = 9/4

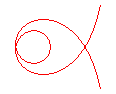
n = 1/5
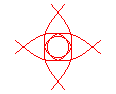
n = 2/5
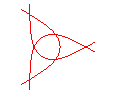
n = 3/5
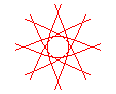
n = 4/5
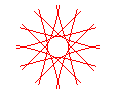
n = 6/5

Pour n petit, la courbe s'enroule autour du cercle de centre O et de rayon a (mais ce n'est pas un cercle asymptote, il y a un nombre fini d'enroulements).
Ci-contre, n = 1/30.

Les épis sont les sections des cônes sinusoïdaux par les plans perpendiculaires à leur axe.
Voir aussi les sinusoïdes sphériques.

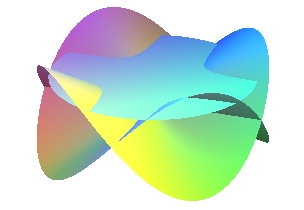Les épis avec n <1 sont les projections des géodésiques du cône de révolution sur un plan perpendiculaire à son axe, le demi-angle au sommet du cône étant égal à .

Les épis sont solutions du problème consistant à déterminer les trajectoires dans le vide d'un point matériel soumis à une force centrée sur O proportionnelle à (cette force est d'après la formule de Binet proportionnelle à qui vaut ici , avec ) ; les autres solutions sont les spirales de Poinsot, avec comme cas intermédiaire la spirale hyperbolique, voir ce lien.

Est-ce parce que le motif de base rappelle la barbe d'un épi de blé que les épis ont été ainsi dénomés ?

courbe suivante courbe précédente courbes 2D courbes 3D surfaces fractals polyèdres

n = 1 : droite	n = 2 : cruciforme	n = 3 : trèfle équilatère	n = 4	n = 5
n = 1/2 : trisectrice de Delanges	n = 3/2	n = 5/2	n = 7/2	n = 9/2
n = 1/3 : trisectrice de Maclaurin	n = 2/3	n = 4/3	n = 5/3	n = 7/3
n = 1/4	n = 3/4	n = 5/4	n = 7/4	n = 9/4
n = 1/5	n = 2/5	n = 3/5	n = 4/5	n = 6/5

Pour n petit, la courbe s'enroule autour du cercle de centre O et de rayon a (mais ce n'est pas un cercle asymptote, il y a un nombre fini d'enroulements). Ci-contre, n = 1/30.
Les épis sont les sections des cônes sinusoïdaux par les plans perpendiculaires à leur axe. Voir aussi les sinusoïdes sphériques.