TRISECTRICE DE MACLAURIN
Maclaurin
Trisectrix, Maclaurinsche Trisektrix

| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
TRISECTRICE DE MACLAURIN
Maclaurin
Trisectrix, Maclaurinsche Trisektrix

| Courbe étudiée par Maclaurin en 1742.
Colin Maclaurin (1698-1746) : mathématicien écossais. |
| Équation polaire : Paramétrisation cartésienne : Équation cartésienne Paramétrisation cartésienne rationnelle : Cubique circulaire rationnelle droite crunodale. Équation polaire dans le repère (A(2a,0), Aire de la boucle = aire entre la courbe et l'asymptote = Les tangentes en O font des angles de |
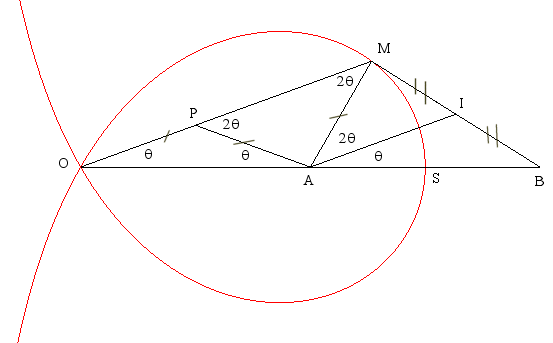
| Deux points O et S étant donnés,
la trisectrice de Maclaurin de sommet S (ici S(3a,
0)) et de point double O est le lieu des points M tels que
OP
=PA = AM où A est défini par L'angle SOM est le tiers de l'angle SAM d'où le nom de trisectrice : si l'on trace une droite passant par A coupant la courbe en M, l'angle AOM fournit le tiers de l'angle SAM. Si B est le point (4a, 0), il est à noter que la médiane (AI) du triangle (ABM) en est alors aussi une trisectrice (le point A voit les segments [MI] et [IB] sous des angles double l'un de l'autre). |
 |
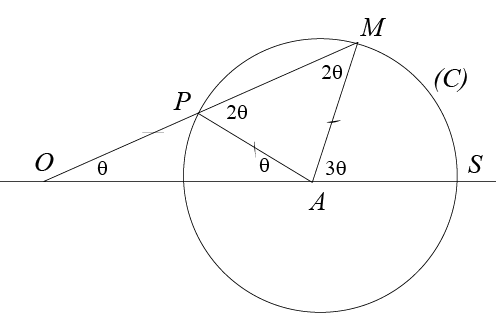
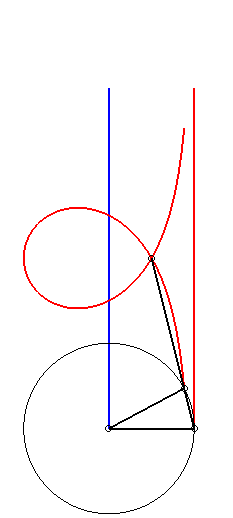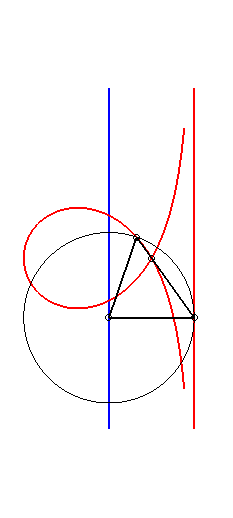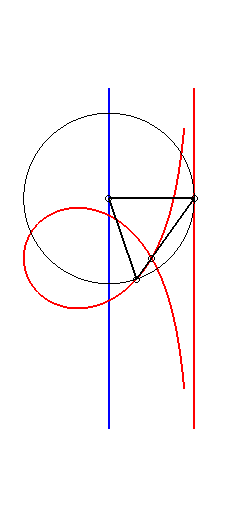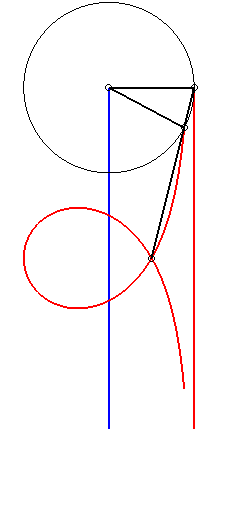
| Maclaurin a imaginé sa courbe à partir
d'une méthode de trisection qui était déjà
connue des grecs : tracer un cercle (C) de rayon R, de centre
A,
passant par S et M ; marquer sur une réglette deux
points O et P distants de R, faire coulisser
O
sur la droite (AS) et P sur le cercle (C) : lorsque
la réglette passe en M, SOM trisecte l'angle
SAM.
Bien que les instruments utilisés soient la règle et le compas, ceci n'est pas une construction "à la règle et au compas" car les points O et P ne sont pas "construits". |
 |
| La trisectrice de Maclaurin est donc aussi le lieu des points d'intersection de deux droites tournant uniformément chacune autour d'un point, l'une ayant une vitesse triple de l'autre (voir la généralisation à sectrice de Maclaurin). |
 |
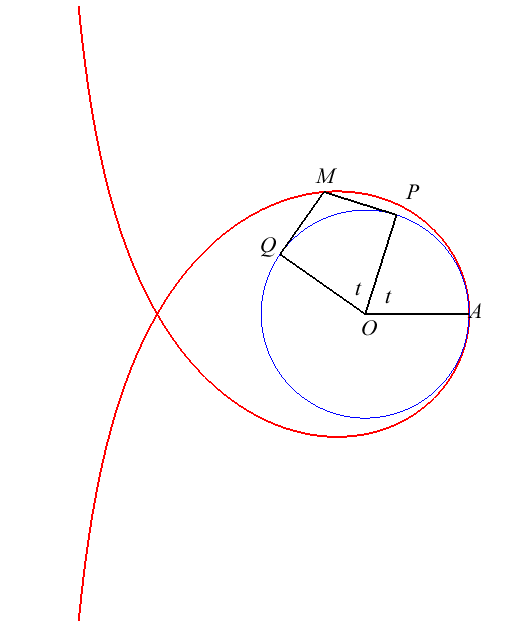
| Autre construction : étant donné un cercle
(C) de rayon a, A un point fixe de (C) ; on
considère un point P variable sur (C) et un point
Q
tel que Le point M a pour coordonnées : |
 |
Comme toute cubique
circulaire rationnelle, la trisectrice de Maclaurin peut aussi être
définie comme :
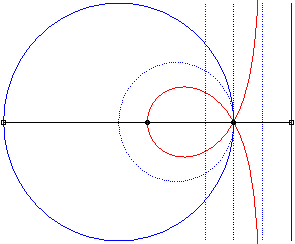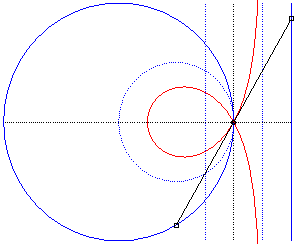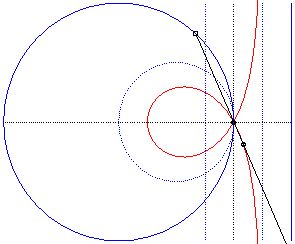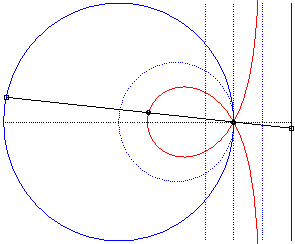
| - la cissoïdale de pôle O d’un cercle passant par O et du symétrique par rapport à O de la médiatrice du rayon issu de O (ici cissoïdale du cercle de centre W(2a, 0) passant par O et de la droite x = – a, relativement à O). |
 |
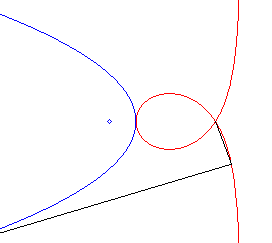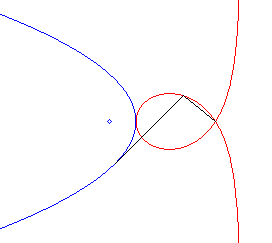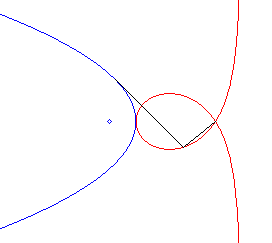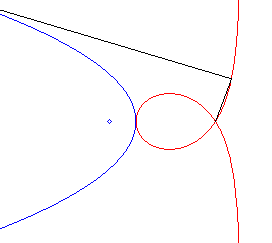
| - la podaire d'une
parabole par rapport au point symétrique du foyer par rapport à
la directrice (ici de la parabole de paramètre 2a et de sommet
S,
d'équation |
 |
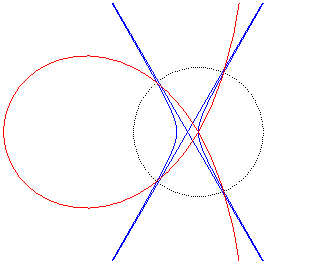
| - l’inverse d'une hyperbole d'excentricité 2 par rapport à l'un de ses sommets (ici, l'hyperbole de sommets O et (a/3, 0)) |
 |
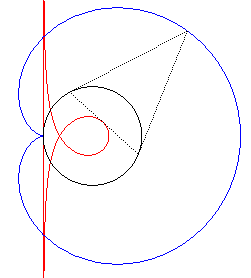
| D'autre part, la trisectrice de Maclaurin est la polaire de la cardioïde par rapport au centre de son cercle conchoïdal : |
 |
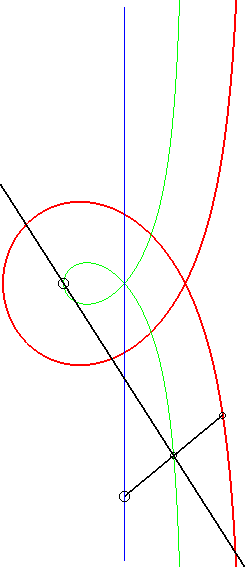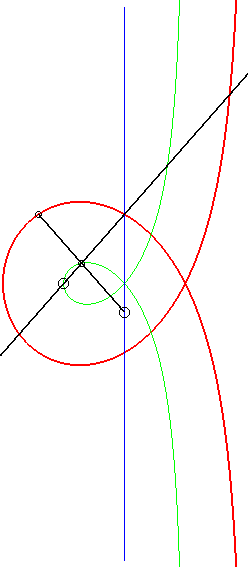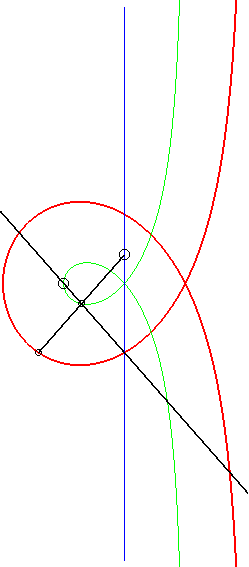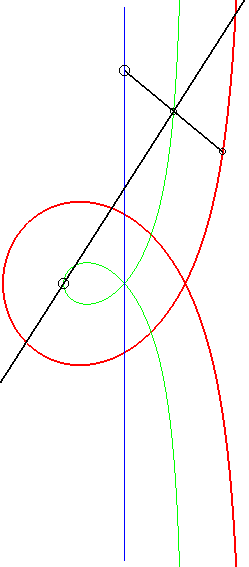
De plus, comme toute cubique
circulaire rationnelle droite, la trisectrice de Maclaurin se construit
aussi
|
|
|
 |
 |
L’équation polaire ci-dessus montre que la trisectrice de Maclaurin est aussi un cas particulier d'épi.
Le folium
de Descartes n'est autre qu'une trisectrice de Maclaurin dilatée.
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2021