Polar equation: . Cartesian parametrization:  (). Cartesian equation: . Rational Cartesian parametrization: . Crunodal right rational circular cubic. Polar equation in the frame (A(2a,0),  ): . Area of the loop = area between the curve and the asymptote = . The tangents at O form angles of  with Ox.

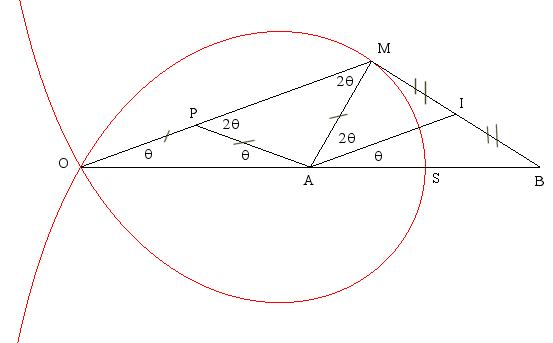
Given two points O and S, the Maclaurin trisectrix with vertex S (here S(3a, 0)) and double point O is the locus of the points M such that OP =PA = AM where A is defined by  and such that O, P et M are aligned. The angle SOM is the third of the angle SAM, hence the name of trisectrix: given the trisectrix and the points A and S, drawing a line passing by A gives the point M, so the angle SOM is the third of the angle SAM. If B is the point (4a, 0), it should be noted that the median (AI) of the triangle (ABM) is then also a trisectrix line (point A sees the segments [MI] and [IB] under double angles one of the other).
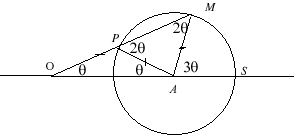
Maclaurin imagined his curve from a trisection method that was already known by the Greeks: draw a circle (C) with radius R and centre O passing by S and M; indicate on a stick two points O and P at distance R from one another, and make O slide on the line (AS) and P slide on the circle (C): when the stick passes by M, SOM trisects the angle SAM. Although the instruments used are the ruler and the compass, this is not a "ruler-and-compass construction" since the points O and P are not "constructed".
The Maclaurin trisectrix is therefore also the locus of the intersection points between two lines, each in uniform rotation around a point, one of them going three times as fast as the other (see the generalisation at Maclaurin sectrix).

Like all rational circular cubics, the Maclaurin trisectrix can also be defined as:
 

- the cissoid with pole O of a circle passing by O and the symmetric image about O of the mediatrix of the radius passing by O (here, cissoid of the circle with centre W(2a,0) passing by O and of the line x = – a, with respect to O).
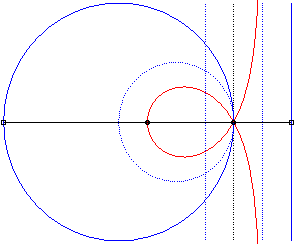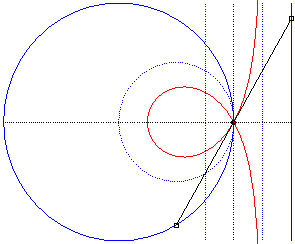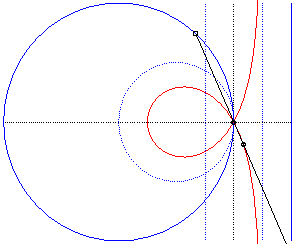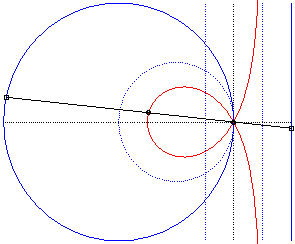- the pedal of a parabola with respect to the symmetric image of the focus about the directrix (here, the parabola with parameter 2a and vertex S, with equation , with respect to O).
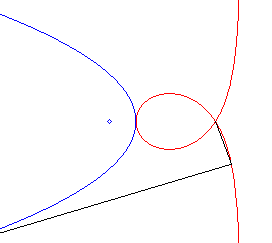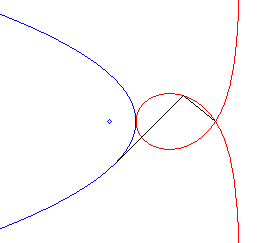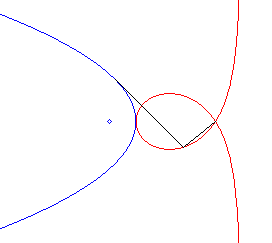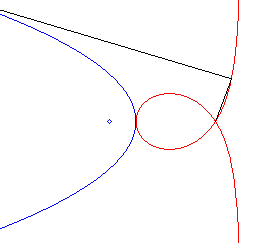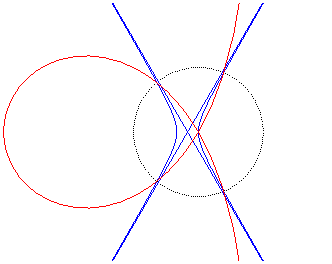
- the inverse of a hyperbola with eccentricity 2 with respect to one of its vertices (here, the hyperbola with vertices O and (a/3, 0))
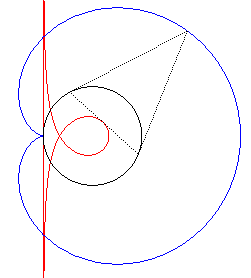
Furthermore, the Maclaurin trisectrix is the polar of the cardioid with respect to the centre of its conchoidal circle:

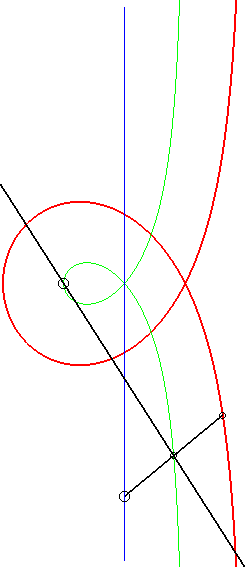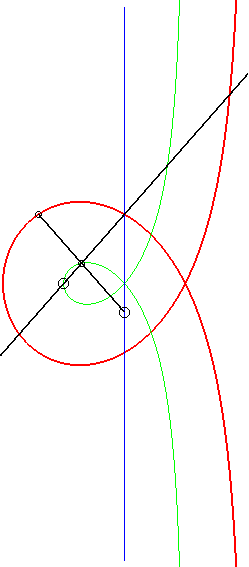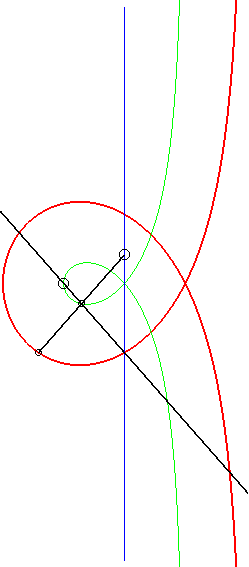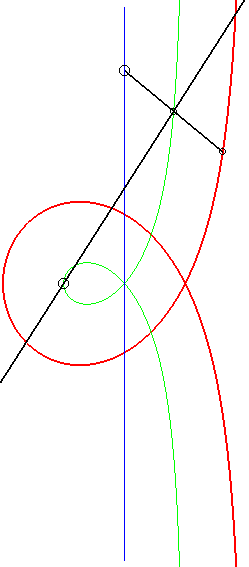
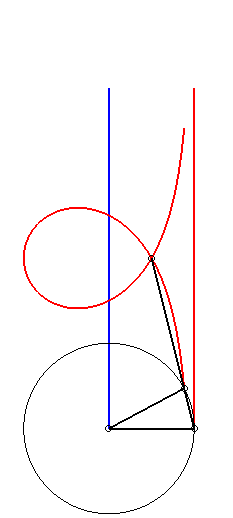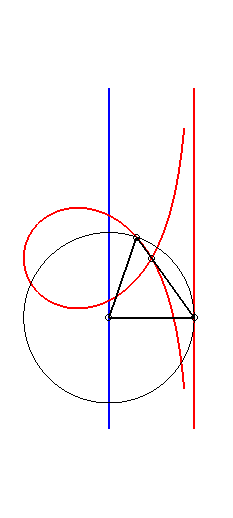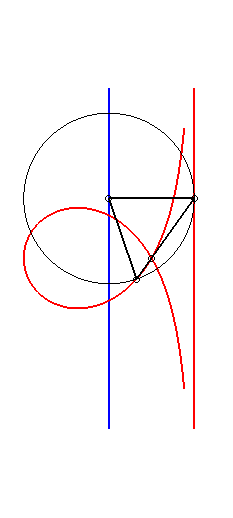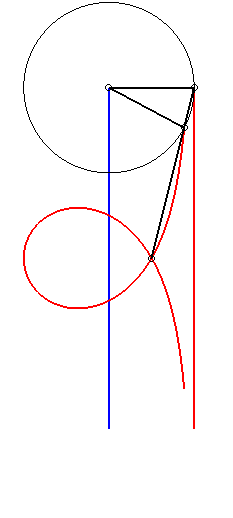
Moreover, like all right rational circular cubics, the Maclaurin trisectrix can be constructed
 

- thanks to the Newton set-square method	- as a kieroid

The polar equation above shows that the Maclaurin trisectrix is also a special case of epispiral.

The Cartesian folium is none other than a scaled Maclaurin trisectrix.
 
 

next curve

previous curve

2D curves

3D curves

surfaces

fractals

polyhedra

© Robert FERRÉOL 2017