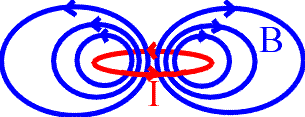
Magnetic field line induced by a circular coil

MAGNETIC FIELD LINE INDUCED BY A CIRCULAR COIL AND A MAGNETIC DIPOLE

See also this article from the union of the physicists.

Since the potential vector of the magnetic field created by a current with intensity I flowing through the curve is , the magnetic field is , and the field lines are given by the differential equation: .
For a circular coil and a point M, we get the coordinates of the potential vector: , and the coordinates of the magnetic field: which, in xOy, reduces to: (Bessel integrals) hence the differential equation of the field lines:
and that of the orthogonal lines:

The curves studied above are the magnetic field lines created by a continuous current flowing through the circular coil with radius a centred on O in the plane xOz, and their orthogonal trajectories:

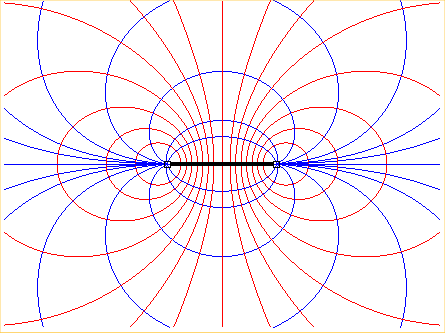
When the point M is far from the coil, the coil is called a magnetic dipole; using the expansion: , we get
the approximate magnetic field:
See another proof at romain.bel.free.fr/agregation/Lecons/LP27.doc
The field lines are then double eggs: , and the orthogonal lines, curves of the dipole, with polar equation .

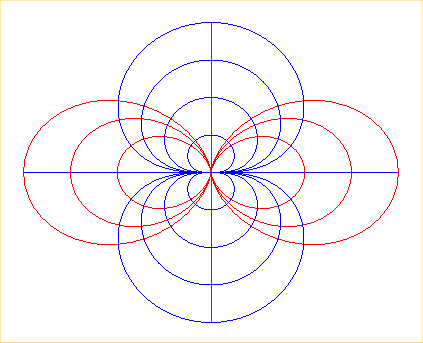
in red, the magnetic field lines created by a dipole, and in blue the orthogonal lines.

Remark: if the coil is replaced by two "infinite" wires carrying currents in opposite directions, the field lines form an intersecting pencil of circles with base points the intersection between the wires and the plane:

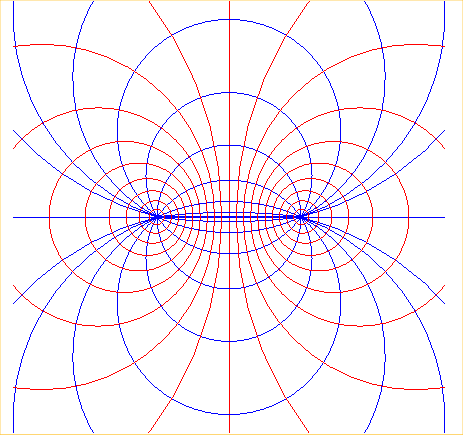
See other field lines here

next curve previous curve 2D curves 3D curves surfaces fractals polyhedra