RIGHT CIRCULAR RATIONAL CUBIC
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
RIGHT CIRCULAR RATIONAL CUBIC

| Other names:
- elongated cissoid of Diocles or right hypercissoid (crunodal case), shrunk cissoid of Diocles or right hypocissoid (acnodal case). - Cramer curve. |
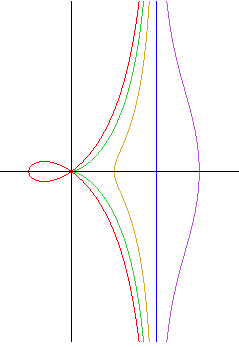
| Polar equation: Cartesian parametrization: Cartesian equation:
|
 |
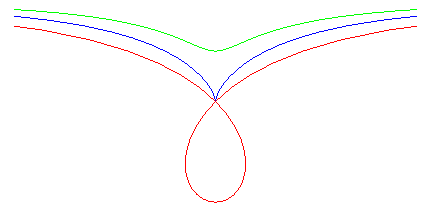
The rational circular cubics are qualified as right cubics when they have a symmetry axis; they are called crunodal, cuspidal or acnodal depending on whether the singularity is a double point with different tangents, a cuspidal point, or an isolated point.
They have the property of being defined by 6 equivalent remarkable geometrical constructions.
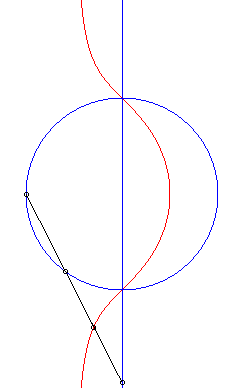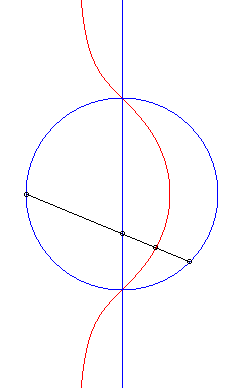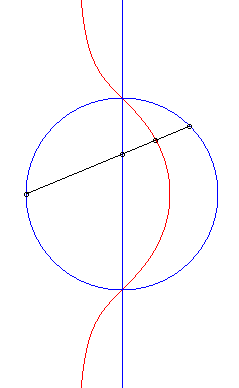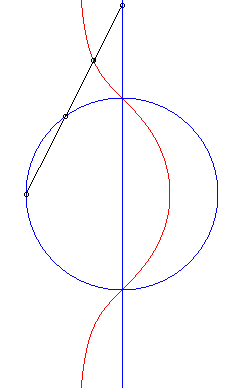
| 1) Cissoidal construction.
These curves are the cissoids of a circle and a line with respect to a point O on the circle, the line being perpendicular to the diameter of the circle passing by O (here, cissoid of the circle (C) passing through O with centre A(b/2, 0) and of the line (D): x = a with respect to O). These cubics, for which (D) is an asymptote and O a singularity, are crunodal, cuspidal, or acnodal depending on whether the line (D'), symmetrical image of (D) about O, is secant, tangent, or outside the circle (C). Opposite, equivalent construction as the polar median of a circle and a line, arising from the equation |
 |
| 2) Construction as a Sluze cubic.
Given a point P describing the line (D), the cubic is the locus of the point M on the line (OP) defined by |
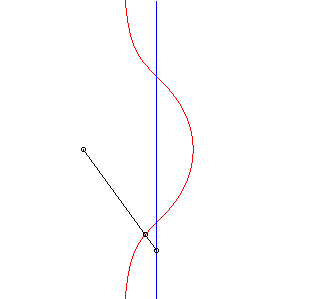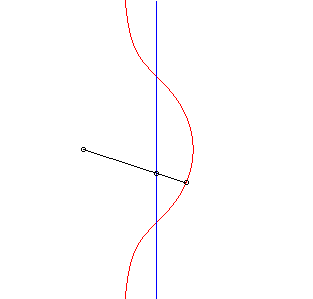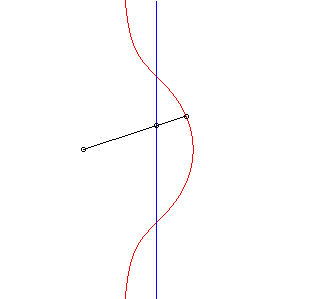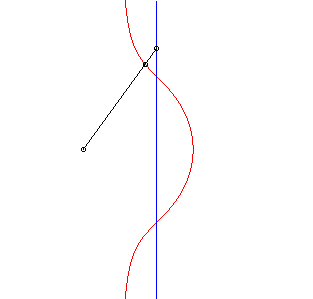 |
| 3) Construction by pedal.
These cubics are the pedals of parabolas with respect to a point O on the axis of the parabola. We get the crunodal, cuspidal, or acnodal case depending on whether the point O is outside the parabola, on it, or inside it. |
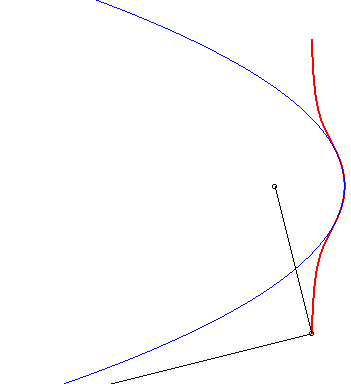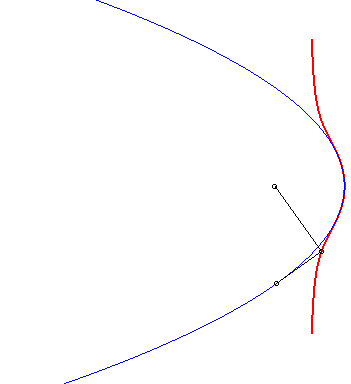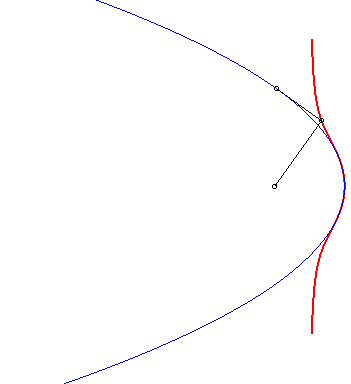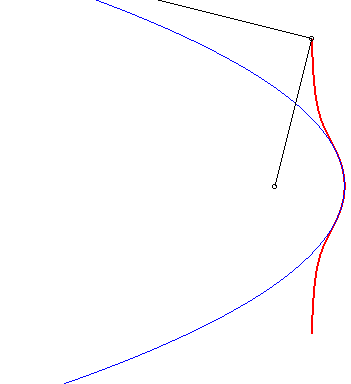 |
| 4) Construction by inversion.
These cubics are the inverses of conics with respect to one of their vertices. The cubic is crunodal, cuspidal, or acnodal depending on whether the conic as a hyperbola, a parabola, or an ellipse. |
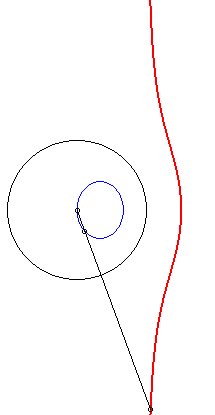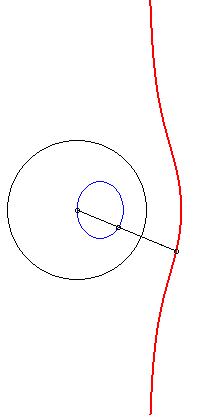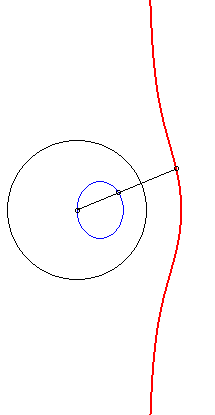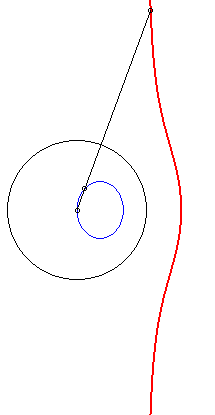 |
| 5) Construction as a kieroid. |
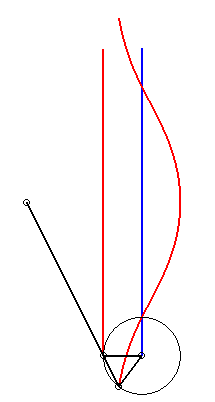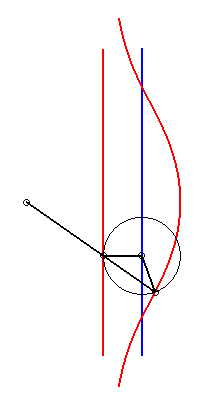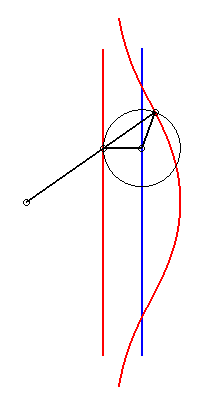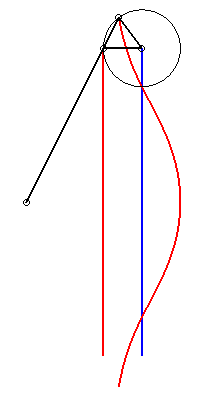 |
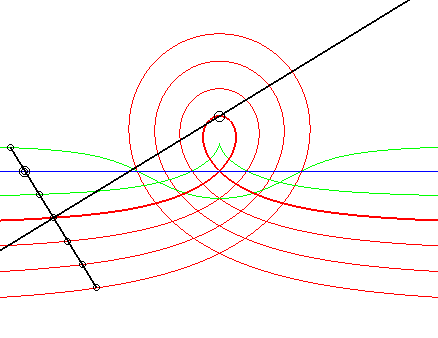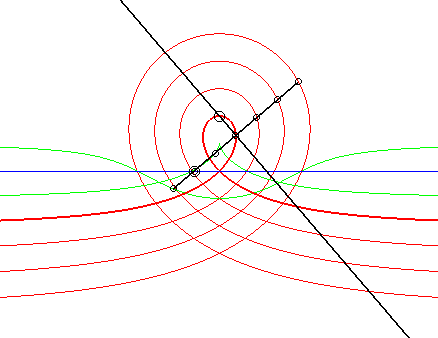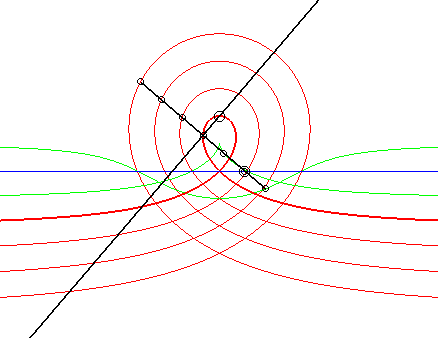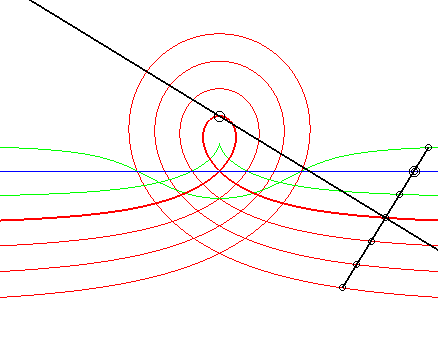
| 6) Construction as a glissette obtained by the Newton set square method.
A movement of a plane over a fixed plane is defined by the fact that a line Dm of the moving plane passes by a fixed point Af and that a point Am of the moving plane describes a fixed line Df, in such a way that the distance between the point and the fixed line is equal to that between the moving point and the moving line.
More precisely, the barycentre M of H, weighted by u, and Am, weighted by 1- u, describes the right rational circular cubic with b = –a u. When M is on the middle I of [H Am], we get the cissoid, when it is on the side of Am with respect to I, we get the acnodal cubics, and when it is on the other side, the crunodal cubics. |
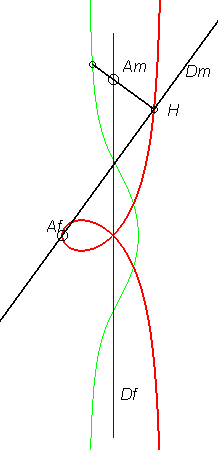 |
 |
 |
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL
2017