Rational quartic (singular point at O) located in the strip
Polar equation:
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
KIEROID
| Curve studied by Kiernan in 1945, hence the name (see
Yates).
P. J. Kiernan: ?? |
| Cartesian equation: Rational quartic (singular point at O) located in the strip Polar equation: |
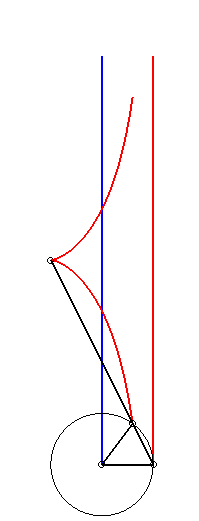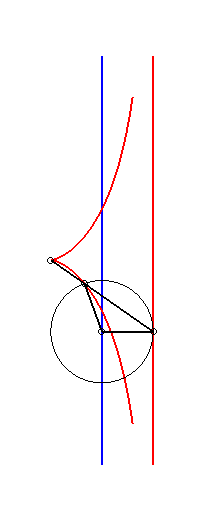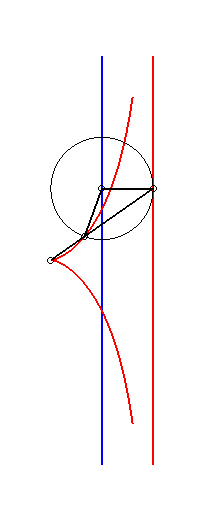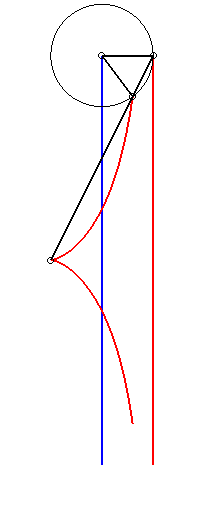
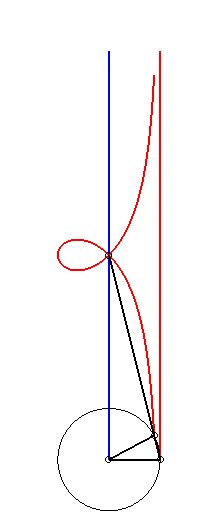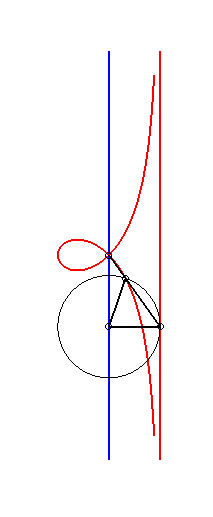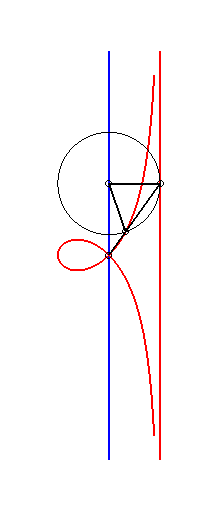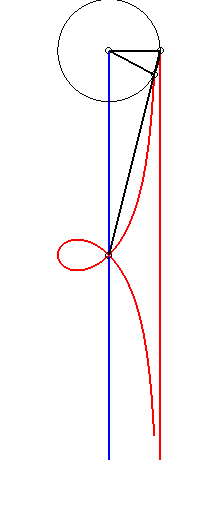
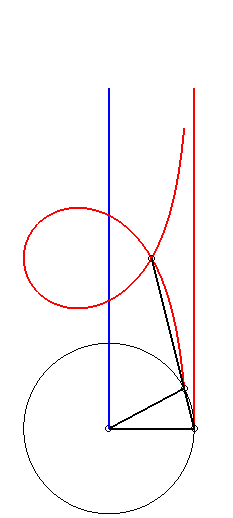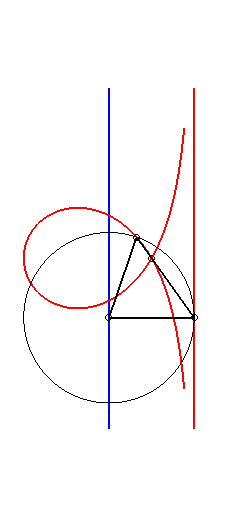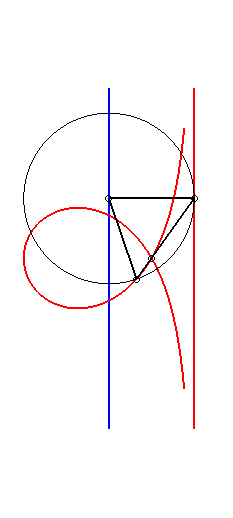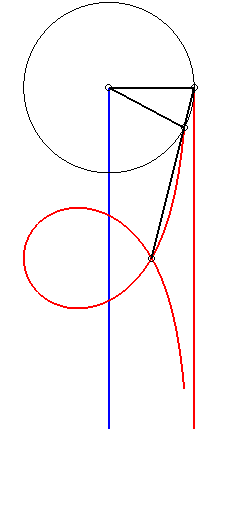
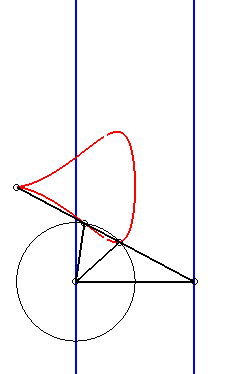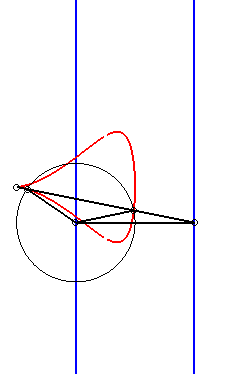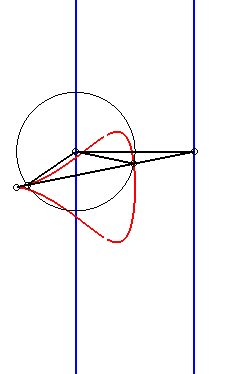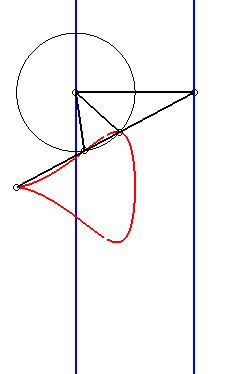
| Given two points N and P with the same ordinate, respectively describing the lines x = a and x = b, the kieroid is the locus of the intersection points between the circle with centre P and radius c and the line (ON). | 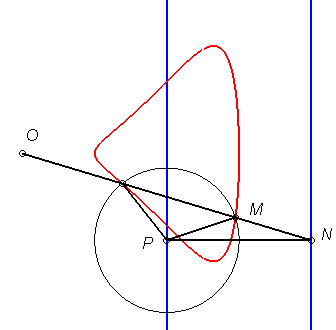 |
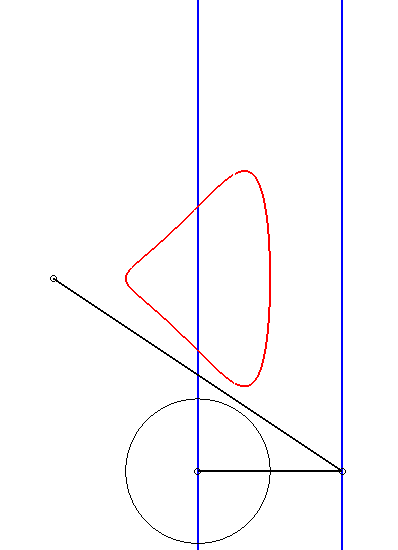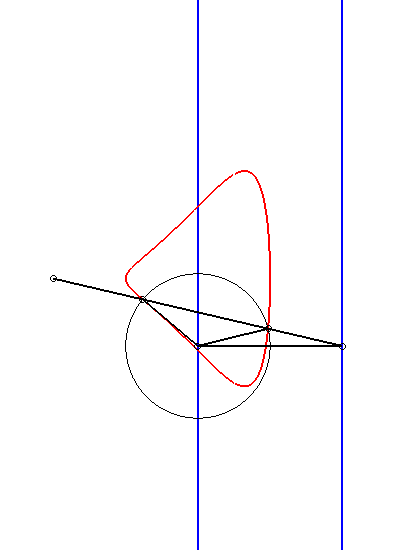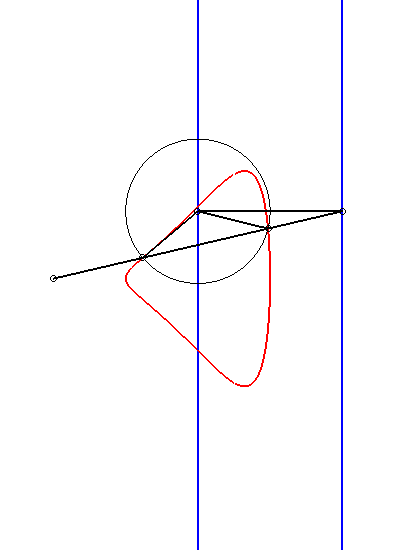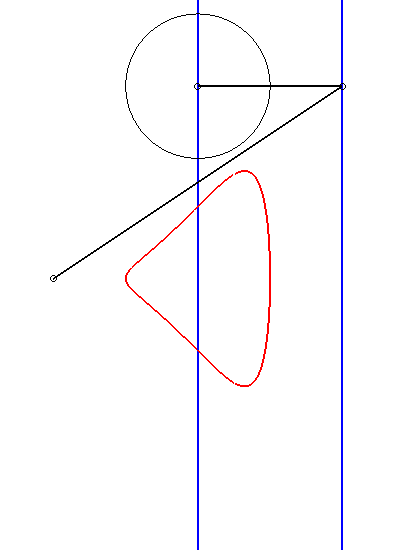 |
When
(i.e. when the circle is tangent to the line x = a) , the kieroid
can be decomposed into a right
rational circular cubic and its asymptote x = a, and all the
right rational circular cubics can be obtained this way, hence a new construction
of these curves.
When a = b+c, the cubic can be written
or
with
the special cases:
| a = 2b = 2c: cissoid of Diocles | a = c, b = 0: right strophoid | 2a = -2b = c: Mac-Laurin trisectrix |
 |
 |
 |
When a = b - c, the cubic can be written 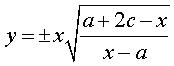 or or |
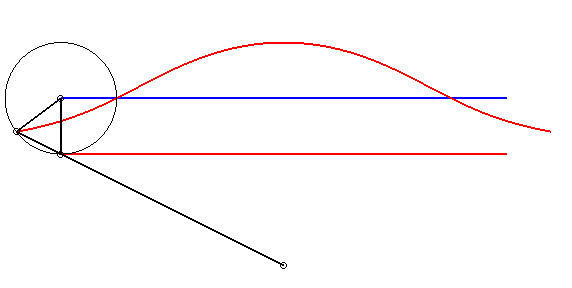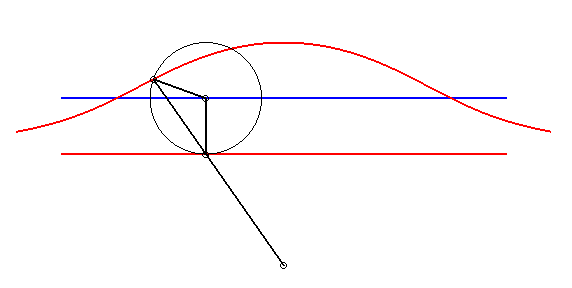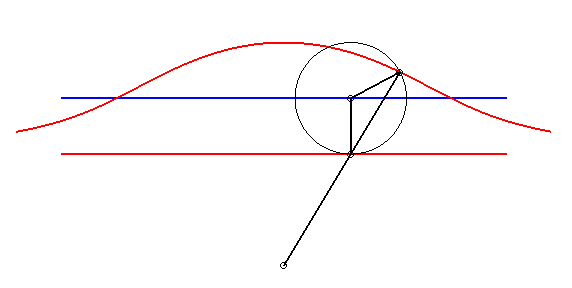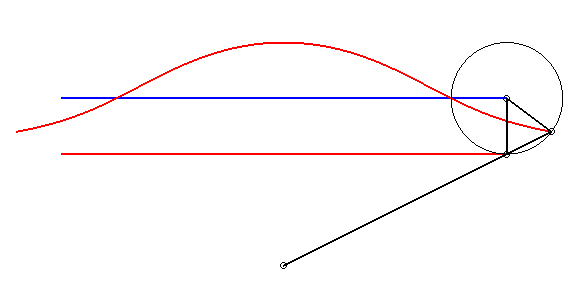 |
| When a = b, we get the conchoids
of lines:
|
When b = c, the kieroid has a cuspidal point at
O; when, additionally, a >> 2b, the kieroid |
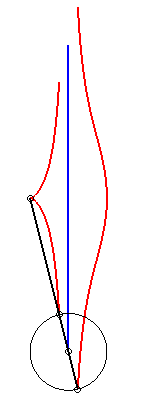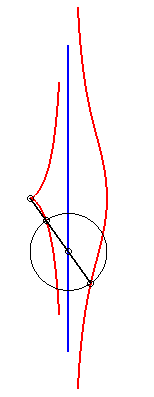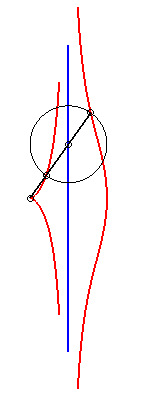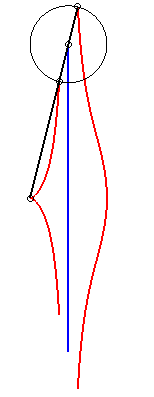 |
 |
Compare to the Rosillo
curves.
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL
2017