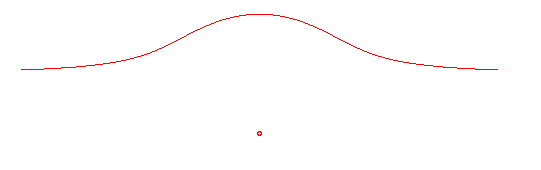
Visiera

VISIERA

Curve studied by Agnesi (1718-1799).
Visiera: visor in Italian.
The name visiera was given by Peano in 1887, probably by analogy with versiera.

Polar equation:

.
Cartesian equation:

.
Right rational circular cubic with an isolated point (-> Sluze cubic)

The visiera is the antihyperbolism of the versiera with respect to its base and the symmetric image of its vertex with respect to its base; in the above equation, the visiera is the antihyperbolism with respect to O and x = a of the versiera: .

Like all rational circular cubics, the visiera can be defined as:
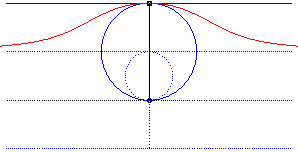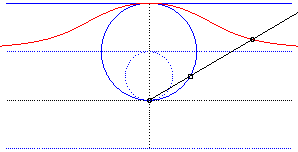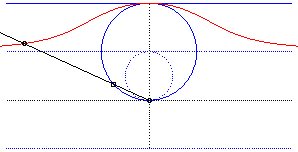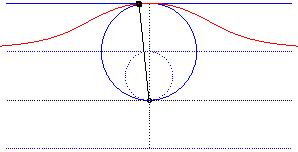
- The cissoid of a circle and a tangent at A to this circle, with pole O, the point diametrically opposed to A (here, A(0,2a)).

- The pedal of a parabola with respect to the symmetric image of the vertex about the focus (here, the parabola with vertex A and focus F(0,a)).

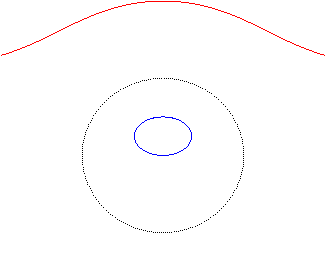
- The inverse of an ellipse with eccentricity with respect to one of its secondary summits (here, the ellipse ).

And, like all right rational circular cubic, it can be constructed

- by the Newton set-square method:	- by the Kiernan construction:

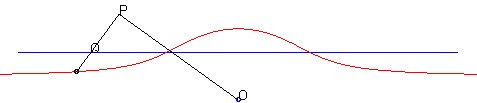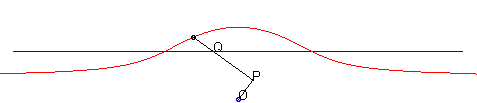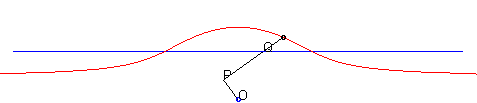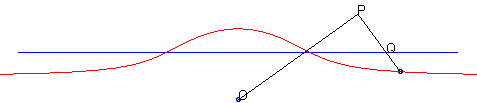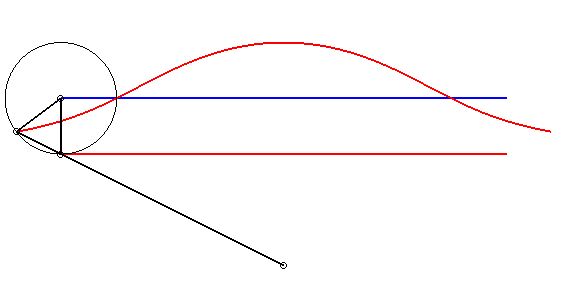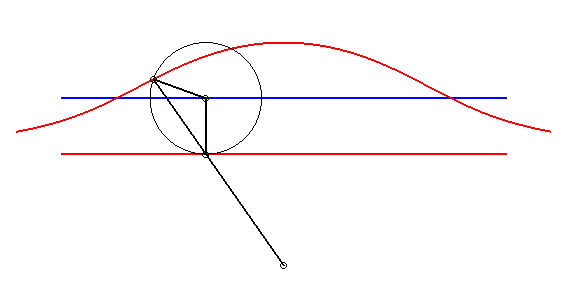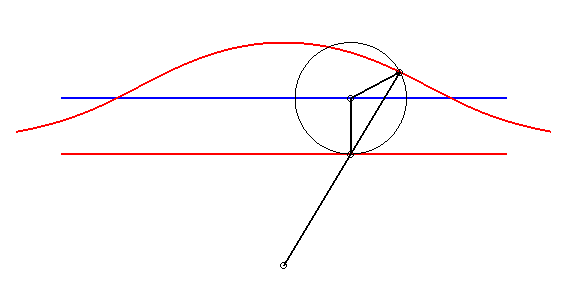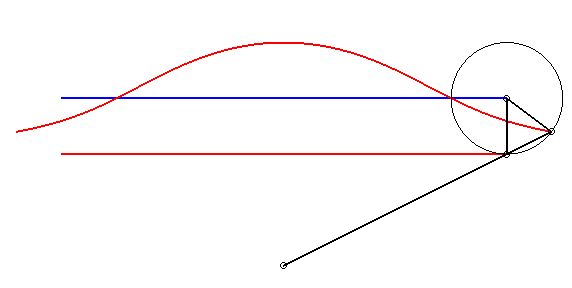Do not mistake the visiera for the conchoid of Nicomedes.

next curve previous curve 2D curves 3D curves surfaces fractals polyhedra