Polar equation: 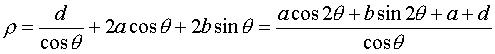. Cartesian equation: ,  i.e., in the case of a right cubic (b = 0): . Cartesian parametrization: . case depending on whether .

The rational circular cubics are the circular cubics that have a real singularity - here, O, which is necessarily unique. The cubic is called crunodal, cuspidal or acnodal depending on whether this singularity is a double point with different tangents, a cuspidal point, or an isolated point.

The rational circular cubics have the property of being defined by four equivalent remarkable geometrical definitions.

1) They are exactly the cissoids of a circle and a line with respect to a point O on the circle (here, cissoid of the circle (C) passing through O with centre A(a,b) and of the line (D):  with respect to O).
They are called right cubics if the diameter passing by O is perpendicular to the line (here, if b = 0).
These cubics, for which (D) is an asymptote and O a singularity, are crunodal, cuspidal, or acnodal depending on whether the line (D'), symmetrical image of (D) about O, is secant, tangent, or outside the circle (C).
 

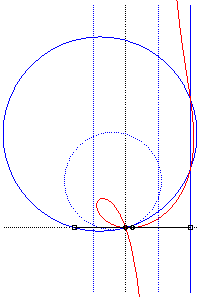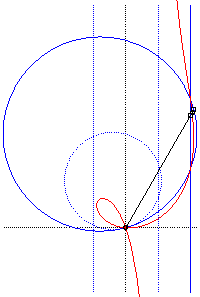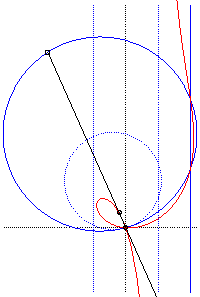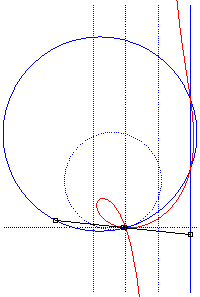
Cissoidal construction, in the crunodal case: in dotted blue, the circle (C) and the lines (D) and (D'),  in blue, their homothetic image of ratio 2, for which the cissoid is the median curve.

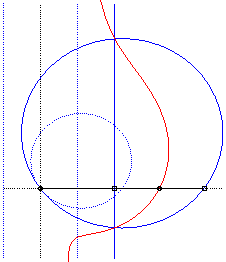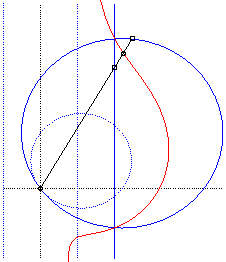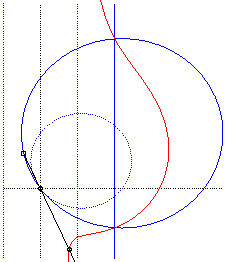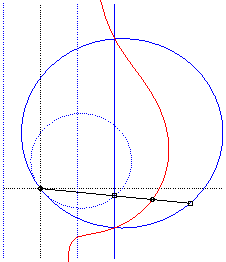
Cissoidal construction, in the acnodal case.

When the line (D') is tangent to the circle (), we get the cissoids;
when it passes through the centre of the circle (d = –a), we get the strophoids;
when it passes through the point diametrically opposed to O (d = –2a), we get the ophiurides;
when it is the perpendicular bisector of the radial segment passing by O(a = –2d, b = 0), we get the Maclaurin trisectrix;
when the line (D) is tangent to the circle at the point diametrically opposed to O (d = 2a), we get the visiera;
In the right and acnodal case, we get the cubics of Sluze.

2)  They are the pedals of parabolas. More precisely, the cissoid of a circle (C) and a line (D) with pole O on the circle is the pedal with respect to O of the parabola with focus F, the point diametrically opposed to O (here, F(2a,2b)), for which the tangent at the vertex (here, x = 2a + d) is the translated image of (D) by the vector ; here, this parabola's equation is .
These pedals are crunodal, cuspidal, or acnodal depending on whether the point O is outside the parabola, on it, or inside it.

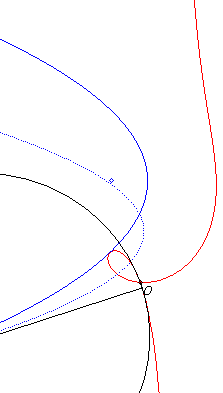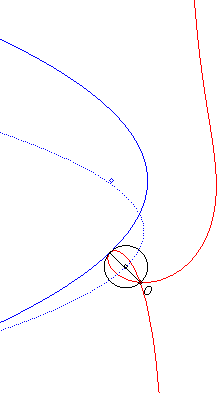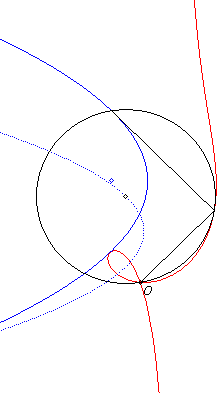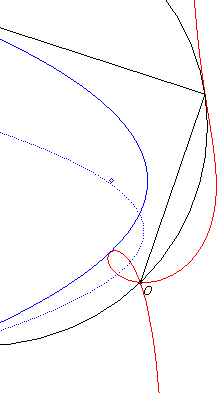
Crunodal case: pedal of a parabola with a pole O extéoutside of it. In dotted line, the initial curve, image of the previous parabola by the homothety with centre O and ratio 1/2.

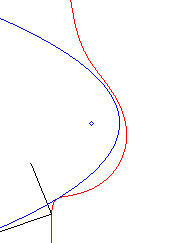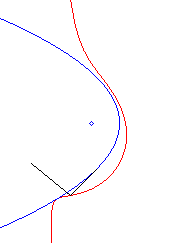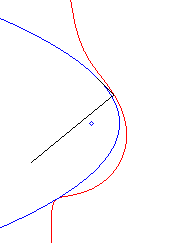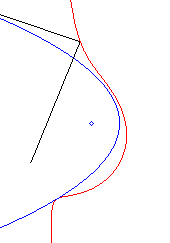
Acnodal case: pedal of a parabola with a pole O outside of it.

3)  Therefore, they are the envelopes of circles with a diameter whose extremities are a fixed point (here, O) and a point describing a parabola (the previous parabola). In other words, they are the cyclic curves with initial curve a parabola, and a power of inversion equal to zero (figure above).

4) They are the inverses of conics with respect to a point on the conic (here, inverse of the conic , where r is the inversion radius, with inversion centre O).
The cubic is crunodal, cuspidal, or acnodal depending on whether this conic is a hyperbola, a parabola, or an ellipse.
 

Crunodal case: inverse of a hyperbola

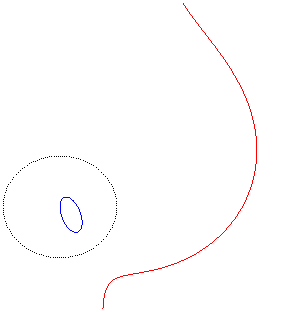
Acnodal case: inverse of an ellipse

See other definitions in the right case.
 

next curve

previous curve

2D curves

3D curves

surfaces

fractals

polyhedra

© Robert FERRÉOL 2017