Ophiuroid

OPHIUROID

Curve studied by Uhlhorn in 1809.
From the Greek ophis "snake" and oura "tail".

Polar equation:

.
Cartesian equation:

.
Rational circular cubic with a double point.

Like all rational circular cubics, the ophiuroids have three geometrical definitions. They are:
- the cissoids with pole O of a circle (C) passing by O and a line (D) the symmetric image about O of which passes by A, the point diametrically opposed to O (here, A(a, b) and (D): x = – a).

- the pedals of a parabola with respect to a point on the tangent to the vertex (here, the parabola with focus A and tangent at the vertex Oy).

- the inverses of a hyperbola with respect to one of its points (here, the hyperbola

, the reference circle being the circle (O, r)).

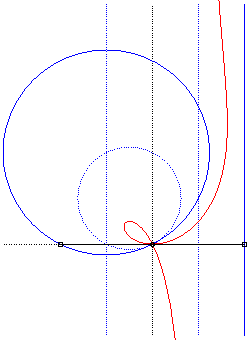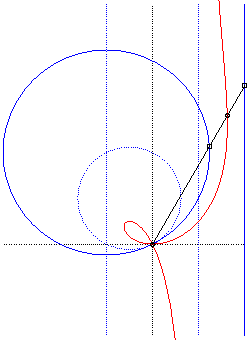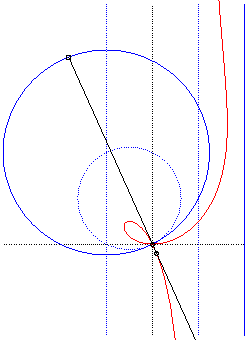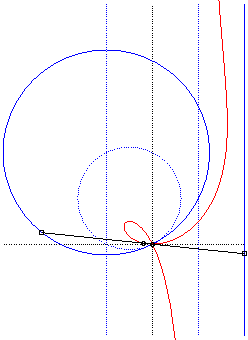
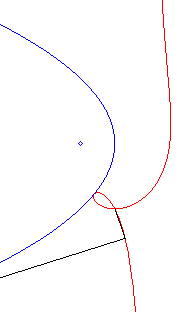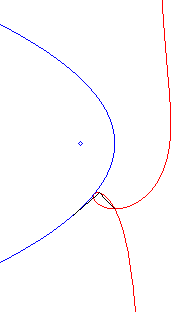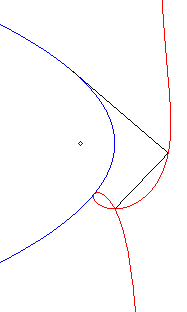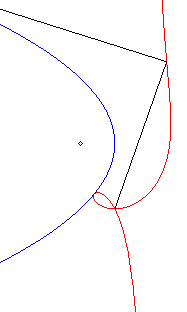
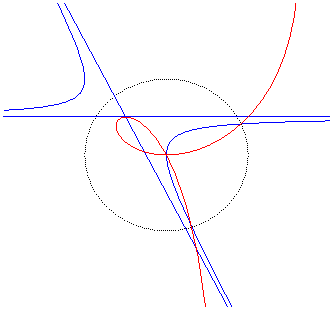
Note that the right ophiuroid is none other than the cissoid of Diocles.

Real ophiuroids!

next curve previous curve 2D curves 3D curves surfaces fractals polyhedra