next curve previous curve 2D curves 3D curves surfaces fractals polyhedra

STROPHOID


Curve studied by Barrow (one of Newton's professors) in 1669, by Quételet in 1810 and by Chasles; the name was given by Enrico Montucci in 1837.
Strophoid comes from the Greek strophos "string, belt, braid". 
Other name: Quételet focal, nodal focal, harmonic curve.

 
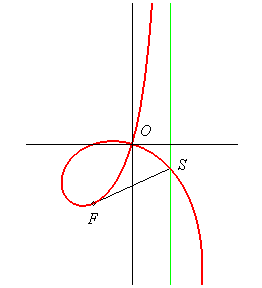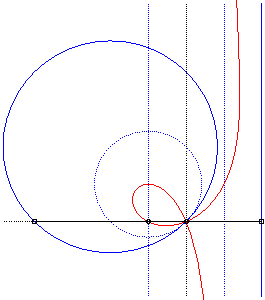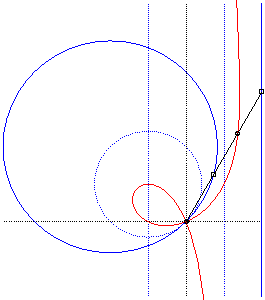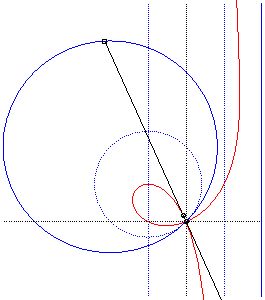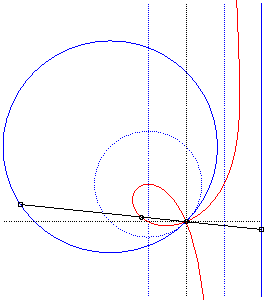
The tangent at the focus F recuts the curve at the intersection point S with the asymptote.		 Polar equation:
with ; 
.  = 0: right strophoid;  = p/2: limit case of the circle.
Focus F ; asymptote : x = a cos ; 
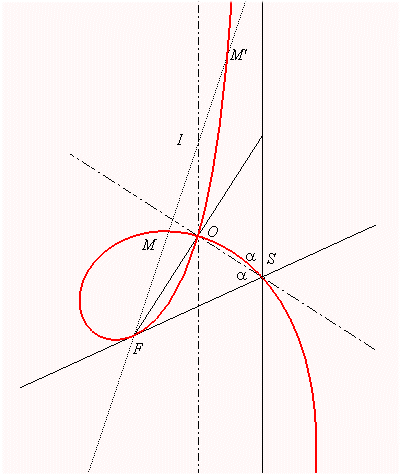
Intersection point with the asymptote: S.
Inflection point obtained for .
Cartesian equation: .
Rational circular cubic with a double point.
In the frame (F , ):
Cartesian equation: .
Complex equation: , with .
Polar equation: , 
i.e., the case + giving the same curve as the case -.
If  and  are swapped, then the polar equation simplifies to:  (so a conchoid of a right strophoid).

 
Given two points O and F and a line (D0) passing by O, the strophoid with focus F, double point O and axis (D0) is the locus of the points M on a variable line (D) passing by F such that PM = PO, where P is the intersection point of the lines (D) and (D0) (in other words, it is the strophoid of (D0) with respect to O and F).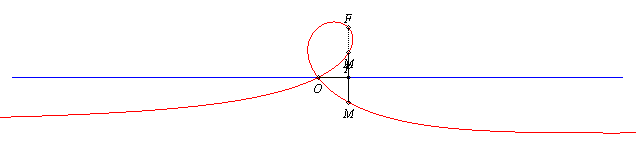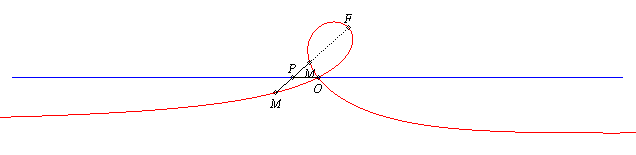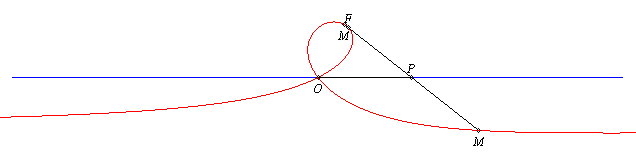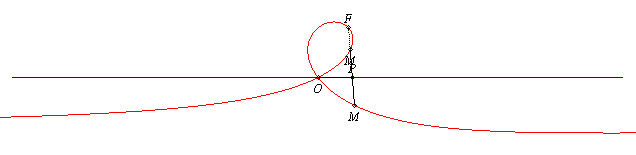
The strophoid is the locus of the points M such that PM = PO
The strophoid is therefore also the locus of the contact points of the tangents passing by F to the circles tangent at O to the axis (D0).

It follows from this definition that the axis (D0) of the strophoid is the median with pole O of the strophoid with itself.

Here, O is the origin of the frame, F is the point , and (D0) is the axis Oy; the asymptote is the line parallel to (D0) passing by the symmetric image of F about (D0).
 
 
Animation showing the construction of the right strophoid by the Newton set-square method, and of two conchoidal strophoids.
See details on the page dedicated to the glissettes.

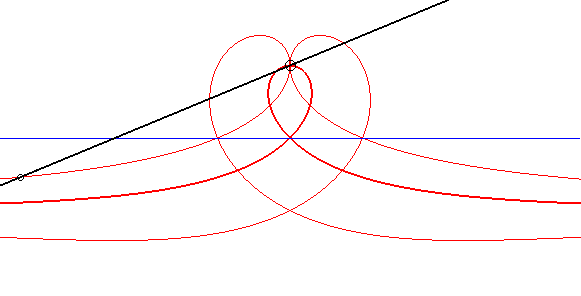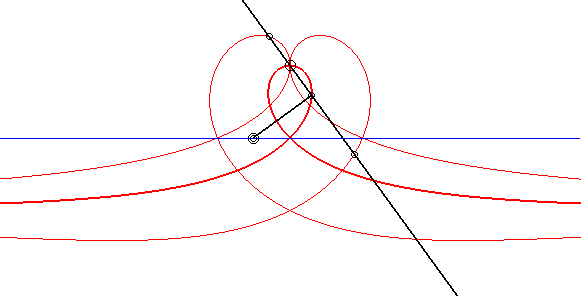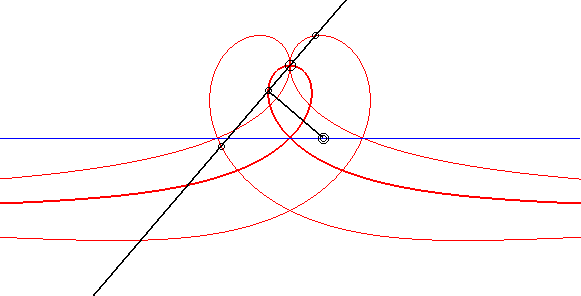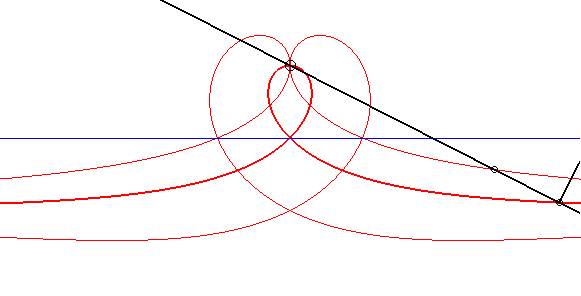The complex equation shows that the strophoids are the loci of the point M such that, if its image by the composition of an inversion with centre F and a reflection about (OF) is called M', then the middle of MM' describes a line (D0) passing by O; M' is called the conjugate of M.
 

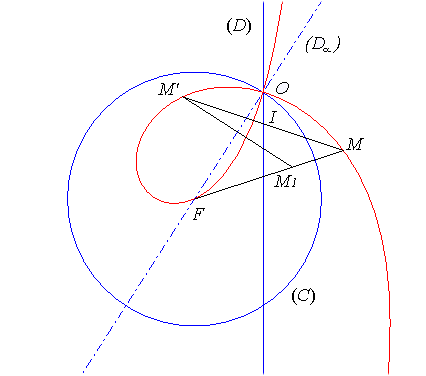The middle I of [M M'] describes the line (D0); M1 is the inverse with pole F of M with respect to the circle (C) and M' is the symmetric image of M1 about (Da ).

If A and A' are two conjugate points of the strophoid, M any point on this curve, then the line (OM) is a bisector of (AMA'); inversely, given 3 unaligned points O, A, A', the locus of the points M such that (OM) is a bisector of (AMA') is a strophoid, and so is the locus of the points M "seeing" the oriented segment lines [AO] and [OA'] under the same angle.
The strophoid is therefore a special case of the isoptic cubic, locus of the points from where two segment lines can be seen under the same angle.
 
A non-flat triangle (ABC) thus gives 3 strophoids:
(SA) defined by (MC, MA) = (MA, MB) in mauve
(SB) defined by (MA, MB) = (MB, MC) in brown
(SC) defined by (MB, MC) = (MC, MA) in green
When the triangle is flat, these loci are circles of Apollonius, hence the name strophoids of Apollonius given to these curves.

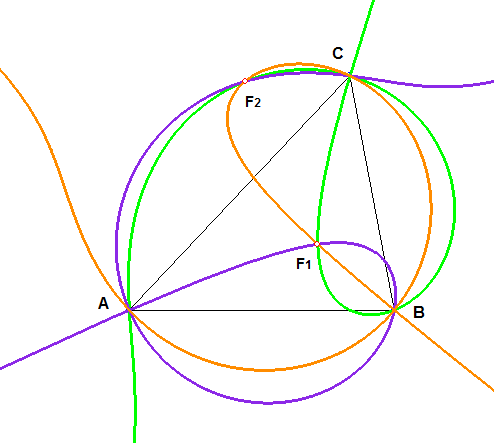The three curves have, in general, 5 common points: the 3 vertices, the Fermat point of the triangle F1 , defined by  if (ABC) is direct, and the second Fermat point F2  defined by . F1 and F2 are the two isogonal conjugates of the triangle.
All the curves also pass by the foot of the altitude passing through the indexed point.
 

 
 
The strophoid is also found in the following optics problem: an observer B looks at the image A' of a fixed point A in a mirror turning around a fixed point O; the locus of the intersection points of the ray BA' with the mirror is a strophoid with double point O, focus A, and axis parallel to (BE) constructed on the figure. If D is the symmetric image of A about OB, then the line (BD) is the tangent at B.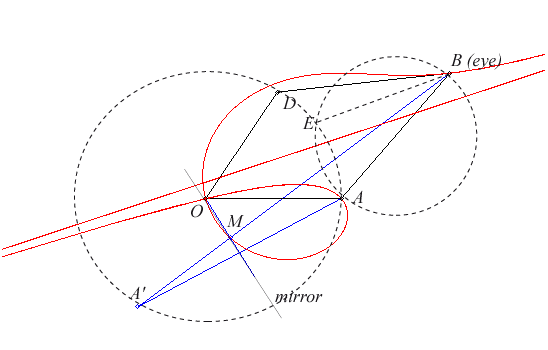

The strophoids have another elegant 3D construction discovered by Quételet, as the locus of the foci of conics (hence the name: Quételet focal): if S is the intersection point between the strophoid and its asymptote, and (C) is the cone of revolution with axis (OS) passing by F (and half-angle at the vertex ), then the strophoid is the locus of the foci of the conical sections of the cone (C) by the planes perpendicular to the plane (OSF) passing by F.
 
S, vertex of the cone, M and M': foci of the conic on a plane perpendicular to (OSF) passing by F; the centre I of the conic describes the axis of the strophoid.
 

For the right strophoid, the cone becomes a cylinder.

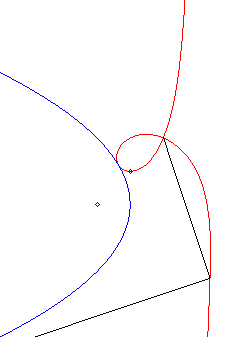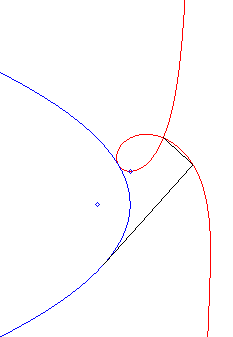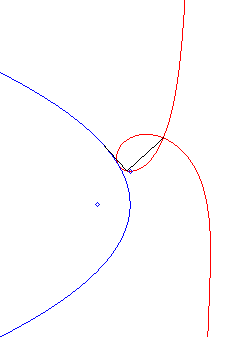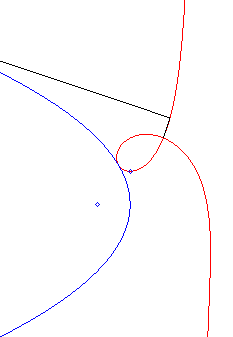
Like all the rational circular cubics, the strophoids can be defined as:

     - the cissoids with pole O of a circle passing by O and a line passing by the symmetric image of the centre of the circle about O (here, the circle is the circle (C) with centre F passing by O, the line, the line parallel to (D0) passing by the symmetric image of F about O).

 - the pedals of a parabola with respect to a point on its directrix (here of the parabola with focus the symmetric image of O with respect to F and directrix the axis (D0) of the strophoid).
The focus of the strophoid is at the middle of the segment line joining its double point to the focus of the parabola.
The strophoid is therefore also the envelope of the circles with diameter joining O to a point on the parabola; in other words, it is the cyclic with initial curve, or deferent, a parabola, when the radius of inversion is zero and the pole is on the directrix of the parabola.

 - the inverses of a rectangular hyperbola with respect to one of its points (here O)

The point F is a singular focus of the curve: the strophoids are therefore special cases of focal circular cubics (hence the name: nodal focal, in other words, focal with a double point).

See cochleoid and Mobius surface.
 
next curve previous curve 2D curves 3D curves surfaces fractals polyhedra

© Robert FERRÉOL 2017