where 
is the pedal of the initial curve, O the centre of inversion and
p
the power.
Condition for the points of the cyclic curve to be real:
.| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
CYCLIC CURVE
| From the Greek Kuklos: circle, wheel. |
| Polar equation:
where
is the pedal of the initial curve, O the centre of inversion and
p
the power.
Condition for the points of the cyclic curve to be real: . |
The cyclic curve associated to a curve 
(the initial curve), a centre O and a power p
is the envelope of the circles (C) the centres of which describe
and such that O has a constant power p with respect to these
circles.
The circle with centre O and radius 
is then referred to as the directrix circle (or circle of inversion)
(C0); the condition
of having a constant power means:
- in the case where p is positive, that
(C) remains orthogonal to the directrix circle.
- in the case where p = 0, that (C)
passes by O.
- in the case where p is negative, that
(C) remains "pseudo-orthogonal" to the directrix circle, in other
words that it cuts it in two diametrically opposed points.
In the case where p is positive, the circle (C) is real only for the points on the initial curve located outside the directrix circle; for the interior points, the portion of cyclic curve obtained only has imaginary points.
Consider the projection N of O on the tangent
(T0) to
at (M0) (N
therefore describes the pedal of
with respect to O).
The two characteristic points M and M'
of the circle (C) centred on (M0)
are the intersection points between (C) and (ON). Therefore,
they are defined by
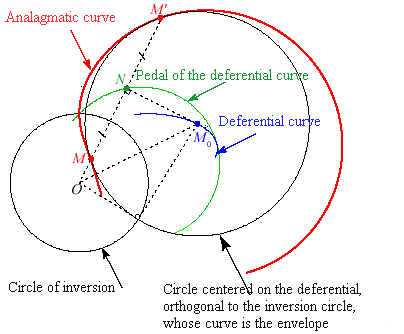
When p is different from 0, the cyclic curve is anallagmatic, with inversion centre O and power p. Conversely, any anallagmatic curve has as many cyclic generations as it has inversion centres.
When p = 0, there is only one characteristic point
M
such that N is the middle of [OM] and the cyclic curve is
none other than the orthotomic
of with
respect to O.
The cyclic curves with initial curve a parabola are the circular cubics (rational if p = 0) and the cyclic curves with initial curve a centred conic are the bicircular quartics (rational if p = 0).
The analogue of the notion of cyclic curve for surfaces
is that of cyclid.
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2017